This post is part of the ppmmc series. Please make sure to have read the previous posts in the ppmmc series so that the context is understood.
A Very Introductory Introduction to Markov Chains — Part 5
In yesterday’s post we were asked to figure out if the Markov Pinball game proposed by Mr. Conner Tist was fair.
Recall the rules
- Let’s say that the game always begins on state 1.
- Every time we land on 4, we lose three points.
- Every time we land on 2, 3, or 5, we gain a point.
- The game ends once we land back on 1.
and recall the state diagram
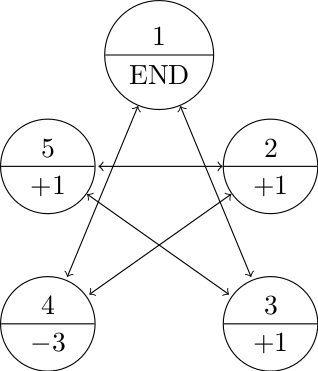
How do we go about determining if this game is fair? It is unlike the dice roll games from a few posts ago. This game doesn’t reset after one step.
One of the things we should do here is try to tinker a bit with the problem. What we want to do is walk through the learning and discovery process about how to tackle such problems. With that said, we know what the large question is, “Is this game fair?”
A good way to get a handle on a large question like this is to first ask smaller questions and to make a number of observations. So, before you read any further, think to yourself and ask questions that you think will help you answer the large question. Remember that just because your thoughts didn’t match up with the author’s thoughts, it doesn’t mean your thoughts are wrong! Also, if your thoughts match up with the author’s thoughts, it doesn’t mean your thoughts are correct! Thoughts are thoughts!
For today’s post, we will show how this is solved “on paper.” Tomorrow we will see what can be verified by simulations.
Getting our arms around the problem
Collecting some thoughts
We know that the game ends when we land back on state 1. The only ways to get back to state 1 are from states 3 or 4. But the only way we can get into state 3 is from state 5 (also from the initial state, but let’s hold off on that condition, we’ll remember it though). And we can get into state 5 from states 2 or 3. And we can get into state 2 from states 4 or 5. We can go through the same logic for state 4. So, clearly as the diagram has indicated all the states are eventually connected.
What if we focused on state 3? What if we didn’t focus on how we got to state 3, but only focused on the fact that we are there. Surely, we have to be able to use memorylessness and time homogeneity in some way. Let’s call \(T_{i}\) the expected number of points accumulated when in state \(i\).
Let’s call \(p_{ij}\) the probability of going from state \(i\) to state \(j\). We know that should be useful at some point, even if we don’t know how to use it.
Now, back to state 3. We could write the expected number of points accumulated in state 3 via this formula (make sure it makes sense!!) $$T_{3} = p_{53}T_{5} + p_{13}T_{1} + 1$$
And here we know that \(p_{53} = p_{13} = \frac{1}{2}\).
This formula says that the expected number of points accumulated per game in state 3 is equal to half the points accumulated per game in state 5 plus half the points accumulated per game in state 1 plus one point because we are in state 3. It is vitally important that this reasoning makes sense. If it doesn’t, get in touch!!
Now, \(T_{1} = 0\) because that’s where the game began and we started with zero points.
But what about \(T_{5}\)? \(T_{5}\) represents the expected number of points accumulated when in state 5. Again, following the same reasoning for \(T_{3}\), we see that we arrive at state 5 either through state 3 or through state 2. So, $$T_{5} = p_{35}T_{3} + p_{25}T_{2} + 1$$
At this point, you may be scratching your head and saying, “but the formula for \(T_{3}\) depends on \(T_{5}\) and the formula for \(T_{5}\) depends on \(T_{3}\), how can that make sense?!” If you are, indeed scratching your head, wonderful! This is exactly what you have to think about. Does that make sense? Why should it make sense? This part of wondering is the math! Everything else is just us monkeying around with calculations. Setting up the formulas through reasoning is what math is about here!
Now, the formulas for \(T_{3}\) and \(T_{5}\) are indeed coupled and that’s no accident. We can get to \(T_{3}\) via \(T_{5}\) and vice versa. For example, a game could go like this: 1-3-5-3-5-3-1
Writing down some formulas
Now, we’ll write down all the formulas following the same reasoning. (Remember \(T_{1} = 0\) and all our transitions probabilities are equal to \(\frac{1}{2}\).)
\[\begin{eqnarray*}
T_{3} & = & \frac{1}{2}T_{5} + 1 \\
T_{5} & = & \frac{1}{2}T_{3} + \frac{1}{2}T_{2} + 1 \\
T_{2} & = & \frac{1}{2}T_{5} + \frac{1}{2}T_{4} + 1 \\
T_{4} & = & \frac{1}{2}T_{2} – 3 \\
\end{eqnarray*}\]
And if we rearrange things so to get rid of the fractions and keeping our unknowns on one side (i.e., our \(T\)s) we arrive at this system.
\[\begin{eqnarray*}
2T_{3} – T_{5} & = & 2\\
-T_{2} – T_{3} +2T_{5} & = & 2\\
2T_{2} – T_{4} -T_{5} & = & 2\\
-T_{2} + 2T_{4} & = & -6\\
\end{eqnarray*}\]
Now, what we have here is four unknowns and four equations. It is a matter of seeing if this system is solvable. But! Before we go on mindlessly solving this. What was the whole point of all of this again? We’ve just been collecting our thoughts so far.
The whole point of this was for us to figure out if this game was fair or not. If we pause for a moment and look at our formulas, we should ask, “How will this bring us to our goal?”
If we can solve the system, we will have the expected number of points accumulated per game at each state. What can we do with that information?
This is where we have to recognize how the game ends. The game ends when we land back on state 1. The only ways to land on state 1 are either from state 3 or state 4. So, if we call \(T_{end}\) the expected number of points accumulated at game end, then our formula would be $$T_{end} = \frac{1}{2}T_{3} + \frac{1}{2}T_{4}$$
Solving
The above system can be solved in any number of ways and the actual task will be left to the reader. The system resolves to the following:
$$T_{2} = \frac{6}{5}$$
$$T_{3} = \frac{12}{5}$$
$$T_{4} = -\frac{12}{5}$$
$$T_{5} = \frac{14}{5}$$
What do these numbers mean? Do they make sense? This is where we should check our intuition against what our calculations showed.
These numbers represent the expected number of points we would accumulate throughout the game for each of the four states. They also seem reasonable. \(T_{2}\) is directly influenced by states 4 and 5. Since coming from state 4 would carry a value of \(-3\), it makes sense that \(T_{2}\) should be small compared to \(T_{3}\) and \(T_{5}\). \(T_{3}\) and \(T_{5}\) are not directly influenced by \(T_{4}\), so it makes sense that their values would be relatively high. In fact, the most likely way to involve \(T_{5}\) in a game would be via 1-3-5-3-1 which happens one out of sixteen times and results in a net positive three points. The next most likely way to \(T_{5}\) in a game would be via 1-4-2-5-3-1 which happens one out of thirty-two times and results in zero points.
Now, our final formula was $$T_{end} = \frac{1}{2}T_{3} + \frac{1}{2}T_{4}$$ and this resolves to zero! Which means that this is indeed a fair game!
For next time
It turns out, at least according to our calculations, that this game is indeed fair. Mr. Conner Tist seems to be telling the truth.
But what if we weren’t able to set up the model that we just set up? You know where this is going. Simulate! That’s what we’ll do next time and we’ll see if our calculations are correct. We will then also see that simulating will give us some additional information that is a bit more difficult to unlock through our mathematical model.
In the meanwhile, it is a good exercise in probabilistic thinking to see if you can understand the formulas and the set up for the game. Just relying on simulations is going to be limiting, especially when (and this will happen) striving for high precision and accurate answers will lead to simulation times measured in eons.
Don’t hesitate to get in touch if you have questions or would like more information about setting up a workshop or training in your school.
One quick note: you will notice that in our system of equations
\begin{eqnarray*}
T_{3} & = & \frac{1}{2}T_{5} + 1 \\
T_{5} & = & \frac{1}{2}T_{3} + \frac{1}{2}T_{2} + 1 \\
T_{2} & = & \frac{1}{2}T_{5} + \frac{1}{2}T_{4} + 1 \\
T_{4} & = & \frac{1}{2}T_{2} – 3 \\
\end{eqnarray*}
if we just add all the equations together we get $$T_{2} + T_{3} + T_{4} + T_{5} = T_{2} + \frac{1}{2}T_{3} + \frac{1}{2}T_{4} + T_{5}$$ which simplifies to $$T_{3} = -T_{4}$$ this combined with our formula for \(T_{end}\) shows that \(T_{end} = 0\)
Moral, here? Don’t think that you are limited to a few canned methods for solving systems of equations.