One of the things I want to do at some point is make a web comic. I’ve taken up drawing this year. If you want to see the progress, you can follow the artwork here.
Here is one of my favorites:

But to make a comic, I need to be able to have artwork that renders nicely on the screen. Additionally, I also have to have consistency in design. Recurring characters need to maintain their appearance over panels and over strips. Some general story-telling is also required.
Of course, my characters are going to have to speak at point. They’ll possibly speak math-y stuff or perhaps quip the things I say in #rantchat. A standard way of showing characters speaking is to use voice bubbles. I’m still hunting around for design. But for something like voice bubbles and thought bubbles, I want a general template. And given that I can program, know a thing or two about math, I figured, what the hey, let’s put those skills to work towards that end.
A classical voice bubble can be viewed as an ellipse with a “fin” protruding in the direction of the character / object that is speaking. An ellipse, generally, is given as $$\frac{(x – h)^{2}}{a^{2}} + \frac{(y-k)^{2}}{b^{2}} = 1$$ where \((h,k)\) is the center, \(a\) and \(b\) are scale parameters that define the ellipse’s shape. When \(a = b\) we have a circle.
So, if I want to make a voice bubble programmatically, I have to draw an ellipse and also draw the protrusion. So, to do this, it helps to make a sketch and label the points we’re interested in.
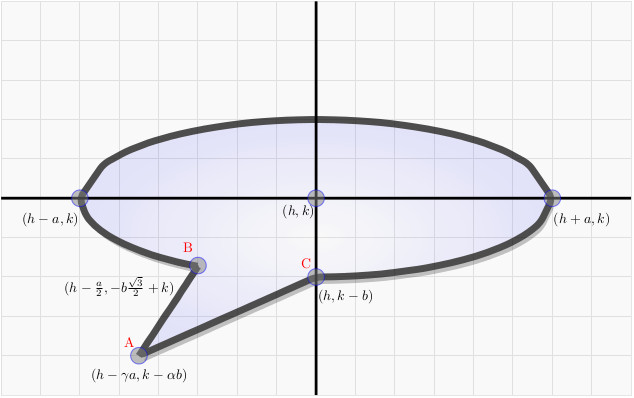
You will notice that there are three special points labeled, \(A, B, C\) with coordinates given relative to the center \((h,k)\). You will also notice that this ellipse is drawn “short and fat”. Short-and-fat ellipses have \(a > b\) and that’s a standard way to draw a voice bubble.
First let’s take a look at point \(B\) with coordinate $$(h – \frac{a}{2}, -b\frac{\sqrt{3}}{2} + k)$$
\(B\) is a design choice. Where do I want to break my ellipse? I figured a good break point would be halfway between the center and the far left endpoint in the horizontal direction. This gives the \(x\)-coordinate of \(h – \frac{a}{2}\). Once we know \(x\) then it’s just a matter of solving for \(y\) from the equation of the ellipse, remembering to take the negative \(y\)-coordinate. So this fixes \(B\).
Next, I made a design choice for \(C\). I just made \(C\) the lowest point on the ellipse. That happens at \((h,k-b)\).
Finally, and most importantly we have the point \(A\)! This is the third point in the not-closed-off “triangle” \(BAC\). The question is where should \(A\) be? Notice that the coordinate given for \(A\) is $$(h – \gamma a, k – \alpha b)$$ The parameters \(\gamma\) and \(\alpha\) control where \(A\) will be. I have imposed a constraint that \(\alpha > 1\) since I want the fin to be below \(C\). Varying \(\alpha\) lets me control where the fin will be vertically. Varying \(\gamma\) lets me control where the fin will be horizontally. Technically, there is a constraint on \(\gamma\) as well in that I don’t it to be so extreme that the fin will so far to the right that it will cross over the voice bubble. But for my purposes, I have a second voice bubble that points to the right. So if I wanted a right point bubble, I would just reflect the left bubble over the vertical axis.
Now what we have to do is figure out some equations. We need three equations: an equation for the line connecting \(A\) and \(B\), an equation for the line connecting \(A\) and \(C\), and an equation for the ellipse so that it traverses from \(B\) to \(C\).
If I use \(A_{x}, A_{y}\) to represent the \(x\) and \(y\) coordinates of point \(A\), respectively and similarly so for \(B\) and \(C\), then the segment \(AB\) for \(A_{x} \leq x \leq B_{x}\) is given as $$y_{AB} = m_{AB}(x – A_{x}) + A_{y}$$ where $$m_{AB} = \frac{B_{y} – A_{y}}{B_{x} – A_{x}}$$
Similarly, $$y_{AC} = m_{AC}(x – A_{x}) + A_{y}$$ with \(A_{x} \leq x \leq C_{x}\)
So that takes care of the fin. And the ellipse we already know to be $$\frac{(x – h)^{2}}{a^{2}} + \frac{(y-k)^{2}}{b^{2}} = 1$$ where we recognize that for \(B_{x} \leq x \leq C_{x}\) we should only take the positive portion.
Now that we have the formulas down, we just have to program it. I used Python because it was straightforward and had the output write to a \(\LaTeX\) file. Then combined with a little bit of tikz magic, I get voice bubbles! The eagle-eyed observer will notice that there is some “jaggedness” to the ellipse. This is purposeful because I didn’t want to have too smooth of a bubble. I can make it smoother by increasing the number of sampling points since the ellipse is constructed by connecting lines at the sampling points.
All the programming and output magic for \(\LaTeX\) import is done in a function I called leftbubble(h,k,a,b,alpha,n). Here n is (loosely) the number of sampling points I want. Partially out of laziness and partially because the look I got was what I wanted, \(n\) is the number of sampling points per section of the voice bubble I want to sample. And because I am being mindful of the order in which I have to traverse the ellipse, I sample from \(B\) to \((h-a,k)\) and then to \((h+a,k)\) and then to \(C\). So, the upper half of the ellipse will be more jagged.
Here are a few samples of left voice bubbles with \(\gamma = \frac{3}{4}\) and varying \(a, b,\alpha\) and \(n\). The figure caption gives the parameters so you can see what happens as the inputs are changed.



There are other things that we can do here. If I didn’t want the fin to be triangular, I could change it’s characteristic so that it would be parabolic. I can also rotate the voice bubble if I needed to. It would just be a matter of adding a few extra lines of code to handle the transformation.
How clean and crisp of a design I want to make is up to me, but now at least I have a general, automatic way of making thematically consistent elements of a comic. I also have something similar for “thought bubbles”, but I’ll write about that later. Perhaps even demo it with a comic!
Pingback: Cartoon Thought Bubbles | Math Misery?