Almost a month ago, @JZagorski1 asked this:
@shahlock Hi Manan, would love to know your thoughts on best ways or program/resources to improve math comp. fluency at el ed level?
— Josh Zagorski (@JZagorski1) August 6, 2015
And now, I’ve finally gotten time to sit down and write some broad thoughts on the matter. Now, I understand that this is a huge topic and one single blog post won’t do it complete justice, but, it is better than replying on Twitter.
There are two main questions in Josh’s tweet: “Best ways” and “Best programs/resources” to improve math computational fluency at the elementary education level. I’ll answer these in a general manner to set up the rest of this article.
Best Ways
Every teacher, good or bad, who thinks they teach Math well, will feel that their methods are ‘best’. A subset of these teachers probably have effective methods of teaching the content and, like any other professional in any other industry, are constantly refining their craft. As such, whatever we deem best, we can likely improve on it. This is part of the teacher’s dilemma.
One thing to remember, at least for this article, is that there is effective teaching (call this Set \(A\)) and then there is effective learning (Set \(B\)). While there is an overlap between these two (\(I = A\ \cap B\)), they also have their separate regions (\(T = A\ \cap \sim B\) and \(L = B\ \cap \sim A\)). Effective teaching could be characterized as clear exposition and organization of content (region \(T\)) as well as creating a respectful environment for learning (region \(I\)). Effective learning could be characterized as high retention of content (and meaning of content) in terms of vocabulary, mechanics, and theory, the ability to pose and answer meaningful questions related to the content (region \(L\)), and the ability to teach the material effectively (region \(I\)).
In this way, we have a feedback loop in (Math) education. Good teaching begets good learning. And good learning begets good teaching (both region \(I\)). But the system is somewhat lossy since good teaching doesn’t guarantee good learning and vice versa. Learning isn’t a brain dump from the teacher to the student. The student still has to do something (region \(L\)). Similarly teaching isn’t simply a scripted set of reactions to student confusion. The teacher does have to actively think about best ways to convey the content (region \(T\))— a point of this article.
Best Programs / Resources
I have generally maintained that the more the teacher knows the less he/she will have to rely on third party content to assist with teaching. I see a lot of “Top \(N\) apps for <math subject topic>” articles and am always perplexed as to why a teacher would build lessons around these products. For example, I don’t need a web or mobile app to teach, say, Arithmetic on my behalf and by and large, nor do students need those to learn Arithmetic. I can teach Arithmetic plenty well and in a myriad of ways, if need be. And students can learn Arithmetic without app gimmickry (euphemism: “interactive learning”). I suppose a goal would be to get students to learn despite themselves — but if that is our main goal, we have other problems.
From a content organization standpoint, third-party resources can be very useful. And much to the dismay of some, textbooks do a fine dandy job of laying out a thoughtful sequence of topics. Once again, the well-versed instructor will be able to modify or rearrange the sequence of topics to his / her preference. Strong content organization, be it in the form of a textbook, pre-set curriculum, etc. can help the less-versed instructor become better-versed. For example, I could teach a standard sequence in Mathematical Analysis, but I really would need a course textbook not just for the organization, but for anchor points for exposition. On the flip side, I absolutely do not need a textbook to teach Algebra, though I use one just to see topic headings. I also tend to rearrange content order when teaching Algebra, but wouldn’t do so with Analysis until I had taught it for a few years.
My point here is that to really learn something — to become fluent — then at some point, the student has to make a study of the topic of interest. And to really teach something, the teacher should continue to make a study of the topic. I still do make a study of Arithmetic — it’s not somehow beneath me because I am a content expert in the topic I have to teach.
So what do we need to build mathematical fluency? And how do we do it?
Elements of Mathematical Fluency
Fluency is tough to define. It’s one of those, “you’ll know it when you see it” kind of things. I’ll argue that mathematical (or any subject) fluency (computational or otherwise) can be broken down into three main categories:
- Vocabulary
- Mechanics
- Theory
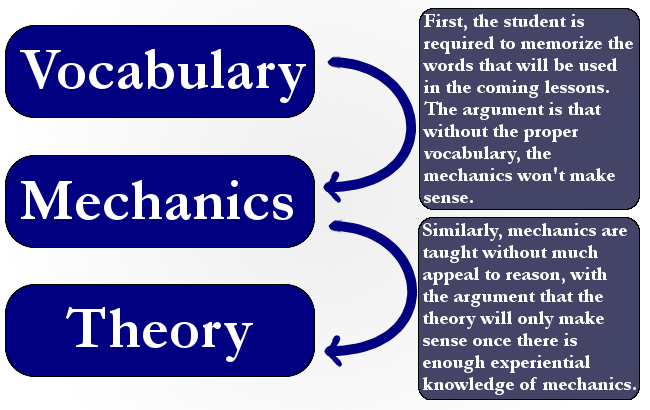
An unfortunate side effect of making such categories is that it leads to an artificial order and a relative disjointedness in teaching the content. For example, I have seen this happen in too many math classes (click for a larger version of the image):
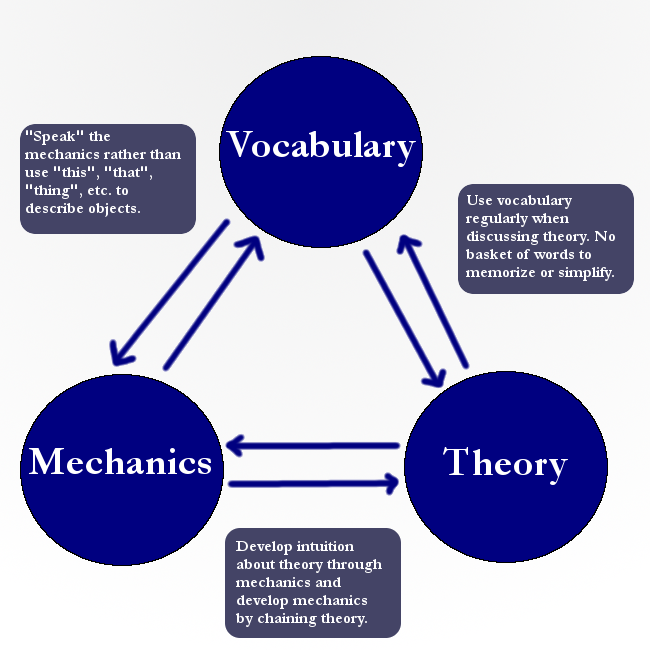
Generally, I find this approach to not be effective in building intuition. The approach I prefer follows a model somewhat like this (click for a larger version of the image):
The idea is fairly simple. If the goal is fluency, then we must have immersion. For example, when introducing elements of graph theory to a group of second graders, I just started using “vertex” and “edge” and constantly pointed to them as I drew on the board. And wouldn’t you know it, in a few minutes, they started using the same vocabulary. There’s no need to simplify “vertex” and “edge” to “dot” and “line”. Students can handle it!
Instructors ought to use vocabulary regularly and steadily get students to move away from “grunting”. When a person doesn’t know how to refer to something, the placeholder ends up being “thing” or “it” or some such equivalent. The separation here is that while the internal model for what needs to be done or what the theory is, may be sound, the external model is unintelligible. This is where the teacher can step in to foster a respectful learning environment by nudging the correct usage (no vocabulary drills are needed, just ask the student to restate the explanation replacing all ambiguous placeholders with appropriate vocabulary). This is also where the student can see the limitations of his/her understanding and by re-explaining with correct usage they are allowed to build a better external model of the mechanics and theory.
One note of caution: math vocabulary may have use only in mathematics. For example, ‘hypotenuse’. So if the student says ‘hippopotamus’ it’s not their fault. They only use ‘hypotenuse’ in a math context. Reinforce the correct usage without shaming.
Similarly, there is no need to require students to memorize algorithms and other mechanics before discussing theory (or vice versa). I’ve found that a constant mix of theory and mechanics helps to build sound intuition about both. For example, when introducing fraction arithmetic, I almost always ask students what they think the result of $$\frac{1}{2} + \frac{1}{3}$$ ought to be. For many students, a natural response is \(\frac{2}{5}\).
The key idea here is to allow students to build a theoretical model through a bevy of examples. People generally pick up on patterns. And too few examples leads to bad pattern matching. \(1 + 1\) is of course equal to \(2\). So if the student extends this general notion of addition (ie the ‘plus’ operator) to fractions, it breaks. And this is a good thing since we can build from their experiential knowledge. If $$\frac{1}{2} + \frac{1}{3} = \frac{2}{5}$$ then is $$\frac{1}{1} + \frac{1}{1} = \frac{2}{2}?$$
In this way, the instructor (a) models how to ask exploratory questions, (b) illustrates the difference between two mathematical objects (integers and fractions (even if they are fractional representation of integers)) and the overuse of the ‘plus’ operator, and (c) nudges the student to come up with a new theory that would keep the existing theory (addition of integers) consistent.
Then the instructor can reveal that $$\frac{1}{2} + \frac{1}{3} = \frac{5}{6}$$ and ask for a new theory of the mechanics. This can be reinforced with more purely mathematical examples or if one prefers, with tangible experiments (eg, how many one-sixth cups can a half cup and a one-third cup fill together?).
In essence, this is a pathway to math fluency. There is no need to start at the vocabulary and proceed to mechanics and then to theory. That is too monolithic of a structure.
Vocabulary, mechanics, and theory are intertwined and the student is better served by bouncing back and forth between the three. What happens is some things become familiar and hence second nature. And those things then act as a launching off point for a next layer of topics to be mastered.
Some Activities For Computational Fluency
Computational fluency doesn’t just mean speed in computation, though speed is a component. I think of computational fluency as the ability to rearrange computation with ease. Before I continue any further, let me address the notion of speed. There is a general objection in some quarters about grading students on speed (eg standardized tests or in-class, timed exams) in the sense that “we’re not measuring understanding” but instead “measuring recall”. While I don’t really care for grading, in general, I will say that speed is a measure of fluency. However, speed comes with fluency and not that “if one is quick then one is fluent”. The objection to speed-based measurement, if I understand it correctly, is that speed often ends up being the only focus to the point that education ends up being nothing more than a series of rote exercises (aka “drill and kill”).
I don’t really have objections to drills. I think they are good for helping to develop the low-level skills for future mastery. How one goes about doing this is an altogether different matter. I prefer computational drills, especially at the elementary education level, to be a mix of entertainment (games) and some straight up contextless questions.
So here are a bunch of games and activities, in no particular order, and certainly not exhaustive, and most certainly not lessons, that I find myself playing with kids or have played as a kid (and sometimes as an adult). I am purposefully omitting the usual stuff like “groceries”, “lemonade stand”, “Monopoly”, sports statistics, etc. I leave it to the instructor to decide if they want this to be speed-based, competition-based, etc. but don’t grade this! 🙂
- Skip counting game: this is actually incredibly difficult from a physical coordination standpoint. Two people walk (skip) side-by-side. One person counts every third step and the other person counts every fourth step. Thus, the counts should go like this: A: 3, B: 4, A: 6, B: 8, A: 9, A+B: 12. A variation is that instead of having the two people walking and counting, the class can be divided into the threes and the fours and they say when their side takes every third or fourth step. Lessons: addition, multiplication, least common multiples. Vary the numbers. Vary the types of numbers (both even, both odd). What happens with three people?
- Lots of dice (Game 1): Take 10 or more six-sided dice (or \(N\)-sided if you prefer) and roll them. What is their sum? What are efficient ways of adding them?
- Lots of dice (Game 2): Take \(k\) with \(k \geq 10\), \(N\)-sided dice and roll them. Using only addition and subtraction, group the dice together so that the sum of the differences is as close to zero as possible. Here is an example with \(k = 4\) and \(N = 6\). Suppose we rolled [3,6,4,6]. If I group them as (6-6) + (4-3), I obtain 1, which is the closest I’ll get to zero. However, if I grouped them as (4+3-6) + (6), then I get 7. As a bonus exercise, ask what the sum of the minuends are and the sum of the subtrahends are. Do their difference tie out with the difference computed? They had better! Why? Did we have to compute the sum of the subtrahends if we knew the sum of the minueds and the overall difference?
- The game of 24
- Or crank it up several notches with “Countdown” — ye be warned when searching YouTube for this … some are NSFW.
- For fractions, I have found using measuring cups to be effective in at least convincing students of why the mechanics ought to be the way they are. But I would encourage the teacher to go beyond simply adding fractions. Ask questions like how many two-thirds cups fit in one cup? This is division! Students can compute the amount by hand first and then see if it makes sense. Any time they have to dump water into the one-cup measuring cup, they can only do it by using the two-thirds cup. They can, however, use other size cups to fill the two-thirds cup. If a sufficient variety of cups don’t exist or are hard to come by, this can be easily mimicked with a ruler and scissors.
- Currency exchange and units — likely better-suited for older students for some ‘real-life’ context and a more involved variation on the typical grocery store exercises. How much does a gallon of milk cost in France? How does that translate to US dollars? Is milk sold by the gallon in France? If you want to avoid currency exchange, then change this up to cost-of-living differences. What is the cost of a gallon of milk in New York City vs Helena, Montana, vs Honolulu, Hawaii?
- The toll plaza — again better-suited for older students. How much does a given toll plaza collect in a day? Does the day of the week matter? How much do they collect from trucks, cars, and motorcycles separately? There is a lot of analysis that can be done here — proportions, expected value, etc.
- The bisection game — it’s a classic, but I don’t see this used in the classroom much: teacher picks an integer from 1 to 100 [inclusive], student(s) have to guess it in 7 or fewer guess. The only feedback the student receives on the current guess is whether it was higher or lower than the teacher’s chosen number. This uses the bisection algorithm, which is basically just division. For added effect, crank up the range and let the teacher demonstrate that 1 to 1,000,000 doesn’t require a bazillion guesses.
These are simple, low- / no- tech activities that are a mix of computational drills and problem solving skills in disguise. Finally, we just have to hope that in-class activities and lessons can be translated back at home. Some of these can be games at home with the family. The bisection game can be a cool little magic trick for a kid to show off. Clearly there are many more such games and activities, but I’m nearly 2500 words.
Pingback: Carnival of Mathematics | cavmaths