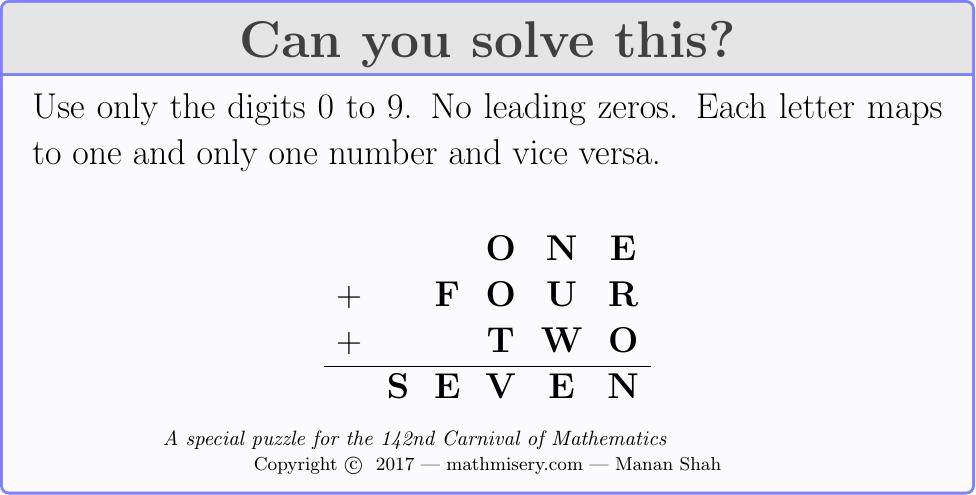So here we are in the month of February, home to Valentine’s Day (2/14), celebrating the 142nd Carnival of Mathematics! Did you notice that 2/14 shares the same digits as 142? As is tradition, let’s first start with a few facts about 142. Here is a mix of random number theory facts and silly facts about 142.

• 142 is an even number.
• All the digits of 142 are powers of 2.
• 142 is a semi-prime since its prime factorization is \(71 \times 2\)
• Unfortunately, 142241 is not prime. However! 1422241 is prime!
• Now, this may seem ho hum, but there’s something cool about \(1 + 4 + 2 = 7\). The cryptarithmetic puzzle below has 8 solutions. Can you find them all?

I’ve been putting up daily cryptarithmetic puzzles. You can check out yesterday’s here.

And so begins the linkfest!

For the most awesome …

We have this submission by Dan McQuillan (@normalsubgroup) about, in his own words,

I thank teachers who do many subtle things with positive—potentially life altering consequences that may not be measured in assessment or exams. I challenge mathematics teachers to consider similar ways that they may affect student’s futures. This requires an awareness of how mathematics questions at lower levels connect to mathematics at higher levels. I use this as a backdrop for introducing a (possibly new) proof of Viviani’s theorem of geometry. I encourage excellent teachers to continue with the methods they believe to be effective, even if pedagogical research makes their methods less fashionable. Memorization is the method example used to make this last point.

Fibonacci and infinite primes

John Cook (@johndcook) shares this, less well-known, proof that there are infinitely many primes. A sharp comment by a reader leads to a minor correction.

When will I use this?

Michael Tang shares his thoughts on a perennial question, “When will I use this?”

A little Calculus

Earl Samuelson (@earlsamuelson) discusses how he introduces integration topics to his high school students in this in depth write-up.

The Mobius function

Over at mathlesstraveled.com, Brent Yorgey explores the Mobius function. This is a multi-part series and I have linked to the first post. I encourage reading this as there is a lot of fun, winding mathematics involved. Maybe this image will want you to check out his writing.

A “Tantonalizing” problem

Brian Hayes (@bit_player) tackles a problem tweeted by James Tanton. It’s a neat little problem, worth checking out! Sorry, won’t give spoilers here! Give Brian’s website a visit!

How many 24 puzzles are there?

Mark Dominus says

This is a really cool correspondence between different-seeming sequences of different lengths. Say that A is the set of sequences of 1..9 of length 4, where the digits must be nondecreasing. Let B be the set of sequences of 1..5 of length 8, again where the digits must be nondecreasing. There are 495 elements in both sets, and this is not a coincidence!

Check it out at blog.plover.com/math/increasing-sequences.html

Exploring sequences

Jim Doherty (@mrdardy) reflects on his Discrete math class and the exploration of recursive sequences. He asks an important question:

How do I help my students focus on building a table of data that is clear and meaningful?

The End!

Well, that’s our Carnival! I hope you enjoyed it. Have you solved the cryptarithmetic puzzle? Leave a comment with your solution(s)!

The next Carnival is at Theorem of the Day. Get your submissions ready!