Well, it’s March and we’re getting battered by snow in the US. Odds are your school will be closed because of snow. There’s plenty of time for formal math learning and if we’re not going to school then we should at least be outside throwing snowballs, trekking through the newly glistening landscape, or just plain enjoying the view and listening to the sound of little bits frozen water falling to their brethern on the ground.
Ah, but eventually, we have to come inside. And maybe we want to challenge our minds a little bit. Just a little bit not too much because we’d like to enjoy our hot cocoa and warm our feet under the blankets.
So here’s a little math game.
- Pick a positive integer. Let’s say \(32\).
- Add the digits. This gives us \(5\).
- Also multiply the original number by 11 and then add those digits. This gives \(32 \times 11 = 352\) whose digits add to \(10\).
- Pick the larger number of \(10\) or \(5\) and repeat from step 2. If you ever find yourself in the situation that both numbers are the same, then the game is over and you win!
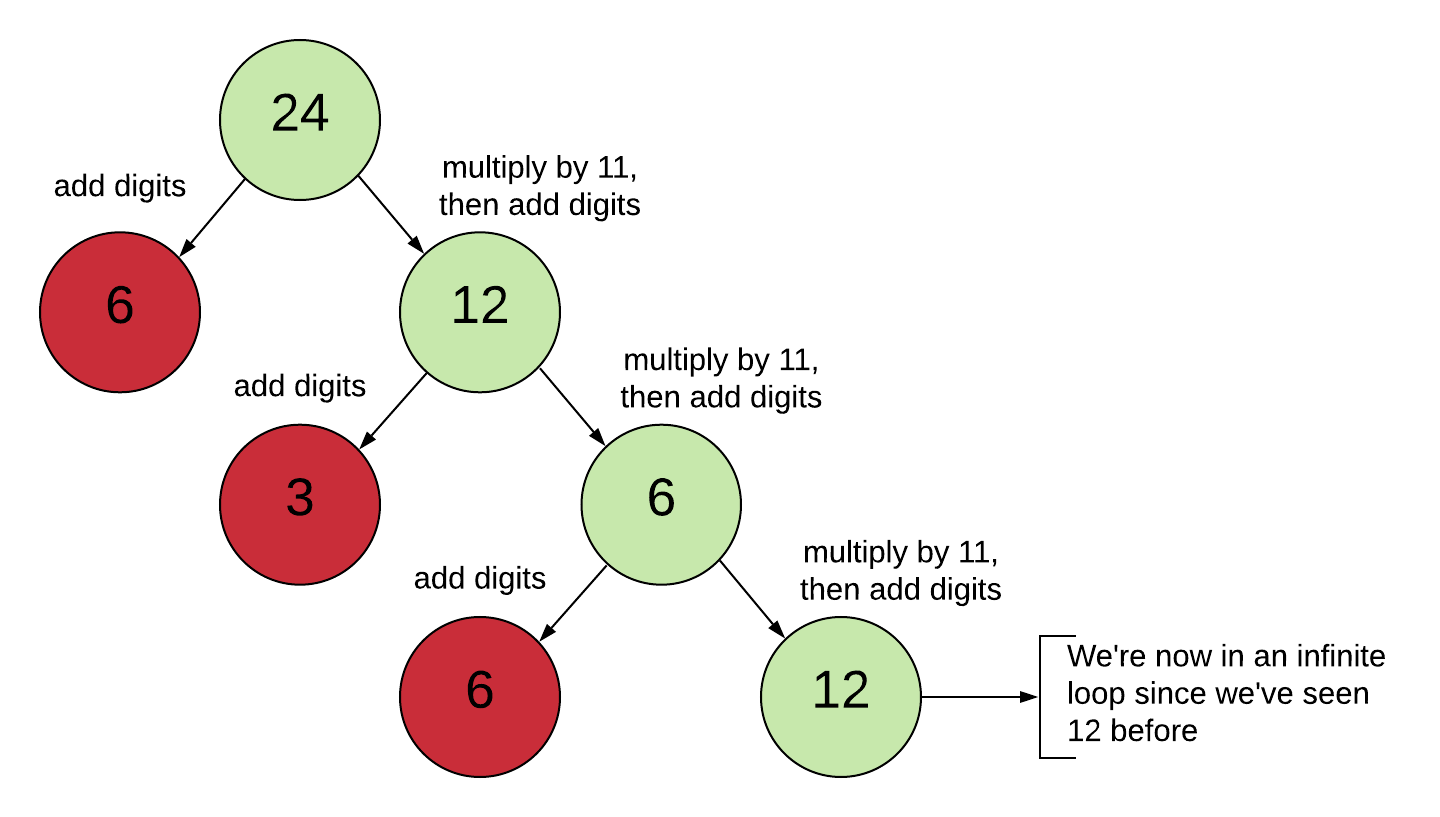
Here’s a visual using 24 for another example.
How many rounds of this does it take to win? Can you ever win? Or do you end up in an infinite loop?
If you find a winning number, let me know! If you can prove that the game is unwinnable, let me know! 😀
A lot of other questions to think about. What do you notice about the patterns of the numbers that arise? Will that pattern always hold? Is this a result of multiplying by 11?
What happens if you change the game to multiplying by 9 instead?