Hey, hey! So what’s so cool about pi? Probably an infinite number of things! Here I want to give you a few fun facts about pi that aren’t directly related to geometry and circles.
So let’s begin!
#1 Buffon!
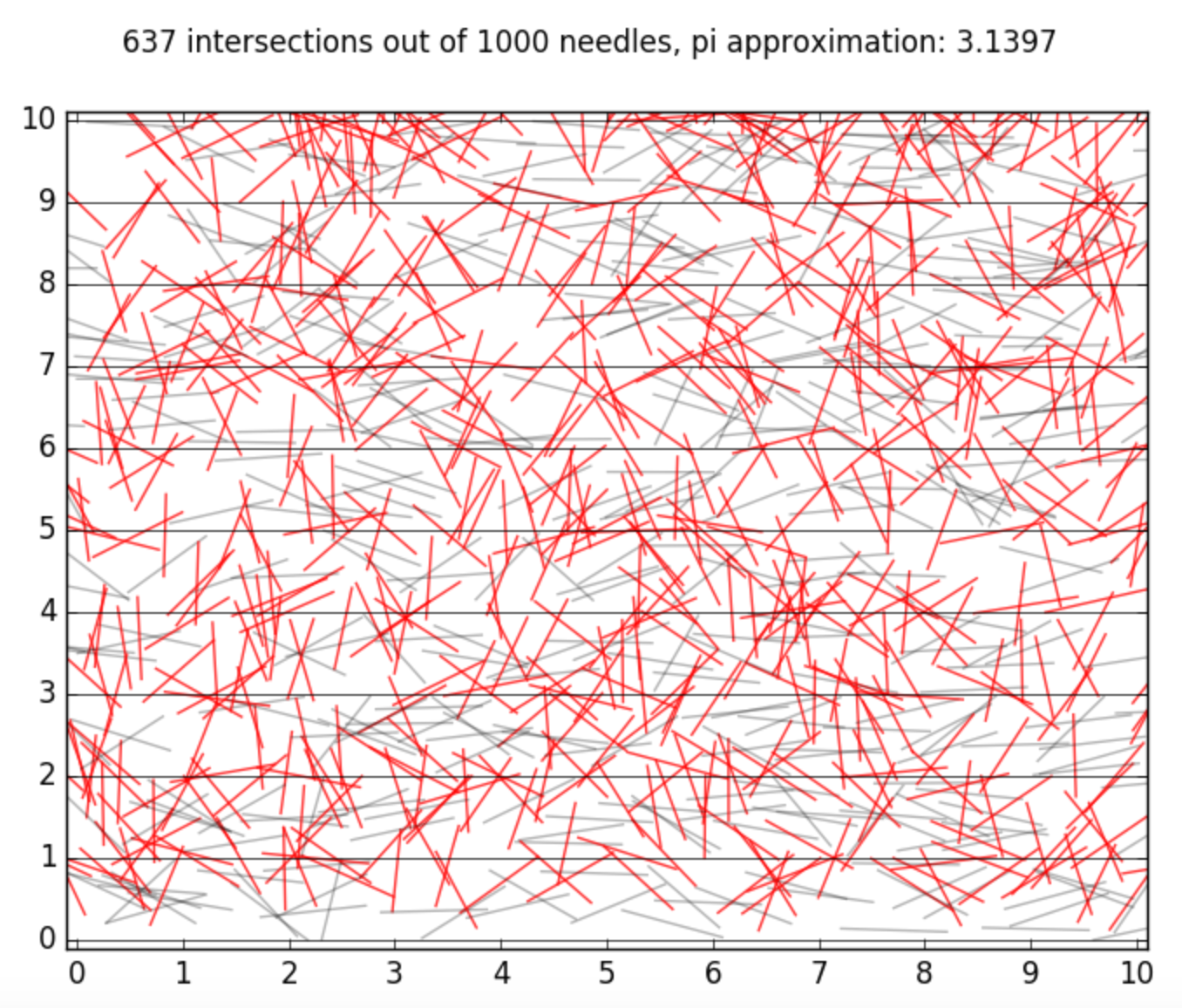
One of the first recorded uses of the Monte Carlo method (before it was even called that!) in a geoemetric setting is now known as “Buffon’s Needle Problem”. Take a rectangular surface with evenly spaced stripes and throw a bunch of needles on it at random. The needles ought to be a specific size. Do this with enough needles and you can approximate \(\pi\)! Here’s one sample:
For further reading, check out: Buffon.
#2 The “Most Beautiful Equation”
Beauty is in the eye of the beholder. However, a 2014 paper concluded that \(e^{i\pi} + 1 = 0\) (Euler’s identity) was indeed the most beautiful equation. This equation uses the mathematical constant \(e\), \(\pi\), the imaginary number \(i\), the number \(1\), and the number \(0\). You decide, most beautiful?
If you want to read about the research, check out this paper.
#3 Infinite Series
Well, we’ve got Euler’s identity, but there are some cool looking infinite series that add up a quantity involving \(\pi\). Here is one particular one that is often a standard problem to prove in a Fourier series course or by use of Parseval’s theorem (or a bunch of other ways).
$$\sum_{k=0}^{\infty}\frac{1}{k^{2}} = \frac{1}{1^{2}} + \frac{1}{2^{2}} + \frac{1}{3^{2}} + \cdots = \frac{\pi^{2}}{6}$$
#4 Actually, my version of beauty
$$\int_{-\infty}^{\infty}e^{-x^{2}}\ dx = \sqrt{\pi}$$
’nuff said.
#5 OEIS Sequence A283247
Guess who is credited with this \(\pi\)-prime sequence? Yours truly!
It begins like this: \(3, 31, 13147, 73141, 314159, 314159, 131415923, \ldots \) — the description of this sequence is “\(a(n)\) is the smallest prime number whose representation contains as a substring the first \(n\) digits of \(\pi\) in base 10.” It’s a \(\pi\) containing sequence of prime numbers!
#6 Speaking of prime numbers
David Radcliffe finds this beautiful (probably) prime number using only the digits 3, 1, and 4!
A 314 prime for Pi Day: A 3141 digit probable prime, with random digits chosen from 3, 1, and 4, starting with 314. https://t.co/rRhv1Ptf2c
— David Radcliffe (@daveinstpaul) March 3, 2019
I had found a measly 463-digit number …
3141143341443144133134133414411314111313431343331433433334311443134444443334411143134144133143343311113144131431144414314114434341444114411144331444113313414341411141314344441344331131143134133343341134333144311444434333413131114414313313441431313131344413411111434331441333134333414431331433444344114341333331334341411434444341431334444114141441131343133314333333334414344411444443111443114141434133414314444133143431111343111313314141314114143331143434131411441
Scavenger hunt question for you! Reading left to right only, how many “314” sequences can you find?
#7 Continued Fraction!
$$\frac4{\pi}=1+\cfrac{1^2}{2+\cfrac{3^2}{2+\cfrac{5^2}{2+\cfrac{7^2}{2+\cdots}}}}$$
Learn more about continued fractions.
#8 A Fun Comparison
Which is larger? \(e^{\pi}\) or \(\pi^{e}\). But let’s add a twist!
Order these four numbers from least to greatest:
$$e^{\pi}, \pi^{e}, e^{\frac{22}{7}}, \Big(\frac{22}{7}\Big)^{e}$$
#9 It’s a little complex
$$i^{i} = e^{-\frac{\pi}{2}}$$
Maybe
#10 It’s not just irrational, it’s transcendental!
\(\pi\) is a transcendental number! And it is unknown if \(\pi + e\) is an irrational number! But I’m putting my money on that that sum is irrational. Learn more about transcendental numbers.