My name is Meredith Valentine. I’m writing this post to recount the tale of Manan’s recent visit to my second grade classroom.
Over the course of several months, Manan and I had schemed and planned about what higher-level math topic he and I might teach to my second graders if he were to visit my classroom. Our goal was to create excitement beyond the basic curriculum that also spans across content areas. Engaging students and creating excitement about learning is what every educator strives for and using community resources, like Dr. Shah, could be just the avenue to do so. After all, a motivated and inspired second grader can grow up to do great things in the adult world!
After several hours of co-planning and preparation, the day finally arrived. Manan visited second grade to do a math lesson! The children trickled into class from their buses and cars, just like any other ordinary day, and began their daily routine of morning work and morning meeting on the rug. When the students returned to their desks from the rug, it was time to introduce our special guest: Manan. Before my students gave me the opportunity to introduce him, there was a buzz about the room with whispers of “Who’s that? Whose dad is that?” or “What’s that person doing here?” Suddenly, an astute 8-year-old shouted out, “Is that the math guy?!” When she got an affirmative response, she replied, “I knew it! You said he was going to come! He’s here!” A quick back story: Manan created a whiteboard application for our class to help celebrate the 100th day. The kids also know that I once beat him at a kid’s card game called “Zeus on the Loose” and that he has worked hard in school for many years to earn a Ph.D. in Mathematics.
During the brief introduction of our special guest, the kids learned that they have a lot in common with this mathematician. They all play an instrument and are good at drawing – just like Manan! Then, I turned it over to Manan and he began to connect with each student individually. It turns out that while the kids were trickling in, Manan was learning their names – an amazing feat – by observing their morning routine as they unpacked, said the Pledge of Allegiance, and completed their community-building hand shake greeting. The connection he created at a personal level was exciting for second graders. Now they were engaged and excited for the lesson to begin.
At first, Manan challenged the kids to organize themselves from shortest to tallest without talking. For the most part, the communication was nonverbal and they achieved success through cooperatively figuring out where each classmate should stand. Upon completion, Manan asked the kids if they were satisfied with the result and began asking questions like, “How were you able to organize yourselves without talking? How did you know where to stand?” The students explained that they stood back-to-back and checked their friends nearby to make sure they were also standing in the correct place. As they returned to their seats, the kids posed the question: Can the adults in the room organize themselves by height? First, Manan and I quickly got in height order, but the children weren’t satisfied. They wanted my co-teacher and supervisor, who was observing this special lesson, to get in on the action. My supervisor enhanced the lesson by asking from across the room for a hypothesis about where they predicted she would stand in the lineup. We discussed why they thought it might be more difficult to predict with accuracy when she was so far away from the other adults. As she got closer to our line, they realized that their prediction wasn’t as accurate as they thought, so they revised their answer. This was good scientific thought!
The vocabulary and concept of self-organizing systems was introduced: “Can your desk organize itself? No! You have to tell it where things go because it can’t do that itself. Your desk is NOT a self-organizing system.” The students began to realize that they could self-organize when provided with a set of rules. Manan took it a step further: “Can computers self-organize?” Some students said no, but one said yes. This student’s response was specific. He said, “Like when you download an app, your computer puts it somewhere. It knows where to put it.” Manan’s reply encouraged this thinking, “Yes! A programmer first has to tell a computer what to do in order for it to understand, organize, and carry out a set of instructions.”
“Would you want to live on Mars or the moon one day?” The kids were shocked by the question and had mixed responses. At first, they didn’t believe that this was even a possibility that some people are hoping will one day become a reality. Since there are people in the world who desire to live on the moon and explore Mars for long periods of time, we asked the kids, “What if an astronaut were up on Mars building a place to live and needed a wrench that he didn’t have? How would the astronaut solve the problem? How would you get a wrench to him?” This discussion was interesting. Knowing my second graders, I had to make sure that I brought some prior knowledge into the mix and relate it back to a “Time for Kids” magazine article we had read earlier in the year about Mars and new space suits that have been developed, as well as a discussion I had had a few days earlier with one student. I directed the next question to this particular student: “Do you remember when we were talking about NASA and what types of impact and inventions they have had on our everyday lives?” He gave an in-depth response recounting our previous discussion about Velcro. NASA has given us a lot of things because the inventions were necessary for astronauts (and the objects that accompany them) in space shuttles due to the lesser gravitational force out in space.
Back to the astronaut’s wrench and building predicament. How would an astronaut get a specific wrench that he needed to carry out a task? The answers were fitting for 2nd graders: He’ll just have another rocket send it up to him. He’ll use a different tool (like Velcro!). He’ll have to go back to get one (from Earth). We explained that these were all valid ideas, but there could be a cheaper and easier solution. Someone could email a file of a wrench to the astronaut. The students were puzzled. How would you email a wrench? One very excited boy who has some at-home experience with programming and coding immediately had his hand in the air, “The astronaut could open the file and download the wrench file to print from a 3D printer. You can actually do that, you know? A person would have programmed a wrench into a file using computer programming and allowed the person to create the tool that they needed.” Excellent answer and perfect segue to our video example of how robots can self-organize.
While preparing for this lesson, Manan and I found a great, short video explanation about Harvard University’s self-organizing systems research group that involved tiny robots.
This visual display of robots doing a task very similar to what they had just done in their self-organizing experiment was powerful. The kids were clearly engaged and interested in what they observed. I took this opportunity to have the students debrief with their table group about what they had just seen, learned, understood, as well as any questions that they had.
The conversation that ensued was dynamic. They asked one another questions and listened to the responses that their peers provided. They respectfully argued when they disagreed or thought there actually was a better answer for the posed question. This is the scientific method and principles in full swing! As an elementary school teacher, you set up your classroom community to interact with just a bit of teacher guidance, so when the lesson actually becomes a thoughtful community discussion, you cheer inside and facilitate all the learning you can without interfering too much. At this moment, not only did I silently cheer, but I also did a little internal dance. Learning was happening! The kids were fully engaged and excited about what they were learning. We discussed as a whole class about what they had seen and learned and how they related it to their new understanding of self-organizing systems.
We cycled the discussion back to that wrench and Velcro an astronaut might need. How would these self-organizing robots be helpful to an astronaut trying to build a home or building on Mars? Another student asked the question: “But if a robot were building with bricks, wouldn’t it get crushed by the heavy weight of the bricks?” Great question! Scientists would have to develop a larger robot that was programmed to self-organize. Manan made a connection between ants carrying 100 times their body weight to the strength a robot might need to have. Manan then asked the class, “Who is going to solve this problem of getting people on Mars? Do you think it’s going to be me? No, but why not? I’m too old. Who’s going to be doing this? You are!” Someone in the room said, “We are?” “Yes! In 20 years, you will be the ones writing the programs to solve these problems. You will be the scientists to create these discoveries! Scientists were second graders once, too, you know?”
Blank stares and dumbfoundedness were on the faces of these 7- and 8-year-olds. When they realized that we weren’t kidding and this was an actuality, the world of possibilities seemed to open right before their eyes. Could one of these young children become excited enough from the seed planted during this lesson to actually be one of those scientists or computer programmers? If you had the opportunity to see the looks on their faces, you’d believe it just as much as we do.
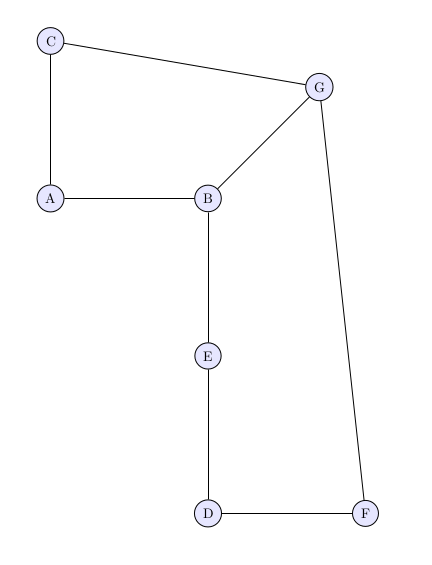
The overarching purpose of bringing a professional mathematician-at-large into our second grade classroom was to get them excited about real-world applications of mathematics. So far, our goal was met with flying colors. The truly exciting part was about to begin: graph theory! The kids were posed with a problem to solve. On the classroom whiteboard, we displayed a set of constraints. They were told that seven of them would have to try to follow the rules on the board and organize themselves into two tables. We also told them that we weren’t sure if this was actually possible to use just two tables. The other students would also be solving and discussing the problem to see if there was an actual solution. A timer was set for four minutes (a purposefully short amount of time). Here were the constraints (student names were used in the actual lesson):
- Student A can’t sit with Student B or C
- Student B can’t sit with Student A, E, or G
- Student C can’t sit with Student A or G
- Student D can’t sit with Student E or F
- Student E can’t sit with Student D or B
- Student F can’t sit with Student D or G
- Student G can’t sit with Student B, C, or F
The children discussed and disagreed and stood near the whiteboard trying to figure out how on Earth to place themselves at two tables. There were so many constraints! Students who were not participants in seating themselves were proudly approaching me with solutions to parts of the problem. One student watching the problem-solving of the group of seven students said: “Just start sitting at tables and see what happens.” Unfortunately, the chimes on the timer went off before they began to sit, so we suggested that they just sit where they believed they should. Then, we checked to see if they had done it by reading the list of constraints. By the time we got through a few constraints, we already had a conflict with the rules. It was time to show one way to solve the problem mathematically – graph theory.
The children learned the appropriate vocabulary of a vertex and edges while Manan and the students together created a graph on the whiteboard. The students quickly understood the procedure and were helpful in creating a solution to the problem. They were fascinated that there was an organized, mathematical approach to solving the seemingly impossible problem that was presented to them just minutes earlier. Through the use of graph theory, it turned out that a viable solution was the need for three tables, rather than two. Instead of simply telling the students that this would solve their problem, we facilitated questions to encourage such a solution. Lo and behold, they said, “Can we just use a third table? I think we need to.” And so we created table number 3. Once a solution was in place, the students reorganized themselves into appropriate table groups. Yet again, science and problem-solving of an unknown were alive and well in a second grade classroom.
In order to close the lesson, we wanted to relate all of this material back to real-life applications. After all, this was the goal and purpose of having a community member join our classroom for the morning. How could people actually use self-organizing systems and graph theory to help them in their jobs? What careers might actually find this helpful? Then, my supervisor shared that she could absolutely use this in her job, but how? The kids guessed that she could use it to plan for classes and teachers and their classrooms for the following year. She shared that she could use it for planning the schedules of all of the classes and students, too. What other professions could use them? “Teachers!”, one student said. “Because they have to seat their students into groups. A teacher does not want too many chatty students at the same table because that would be too noisy and they wouldn’t be able to teach. It would also be too distracting for the other students to learn.”
Before we moved on to our next lesson for the day, I created a little more excitement for other real-world applications. “Today, we used these math concepts that were related to computers and science. Guess what? The next lesson we’ll do related to this has to do with Social Studies” (as I pointed to our wall map). “Really?! You can use graph theory and math to make maps? Wow!” I had them hooked for a follow up lesson – all about math and maps. As we walked through the halls to their next activity, the conversation continued with enthusiasm – they wanted to know more! Our next lesson would be to use graph theory to carry out the Four Color Theorem for which the students would be equally as excited. (A blog post about that lesson will follow as the next in this series.)
In addition, the students begged for two things: 1. Can we please rearrange our seats using graph theory? 2. Can we have more graph theory for homework? I consider those to be dramatic indicators of a successful lesson.
Better yet? I received an email from a parent with thanks for helping her daughter become excited at home about real-world math applications.
Thanks for your time and expertise, Manan. The students, administrators, parents, and I welcome you for a classroom visit anytime.
Meredith Valentine is a second grade teacher. She has been teaching for 13 years and absolutely loves to get up for work each day.