If you are teaching how to solve quadratics and you have gotten to the quadratic formula and are looking for some enrichment, then this article is for you!
For this activity we are going to focus on quadratics of the form $$x^{2} + bx + c$$ where \(b\) and \(c\) are real (and so the coefficient for \(x^{2}\) (typically represented by \(a\)) is 1).
Finding roots of a quadratic can be done in an unconscious way by substituting the coefficients into the quadratic formula $$\frac{-b \pm \sqrt{b^{2}-4ac}}{2a}$$
It’s sometimes helpful to step back a little and analyze the components of this formula. We often refer to $$b^{2}-4ac$$ as the “discriminant”. With \(a = 1\) this becomes \(b^{2}-4c\). Now, most students by this point are either taught “you can’t take the square root of a negative” or “the square root of negative numbers yield imaginary numbers”. The former is the mantra when complex numbers are out of scope and the latter is typically a reminder once students have experienced imaginary / complex numbers.
As a consequence, students know (are taught (not necessarily the same thing)) that if \(b^{2}-4ac \geq 0 \) then the solutions will be real otherwise solutions come in complex conjugate pairs (because of the \(\pm\)). What we often don’t do when teach this is a small excursion in looking at \(b^{2}-4ac\) for various choices of \(a,b,c\).
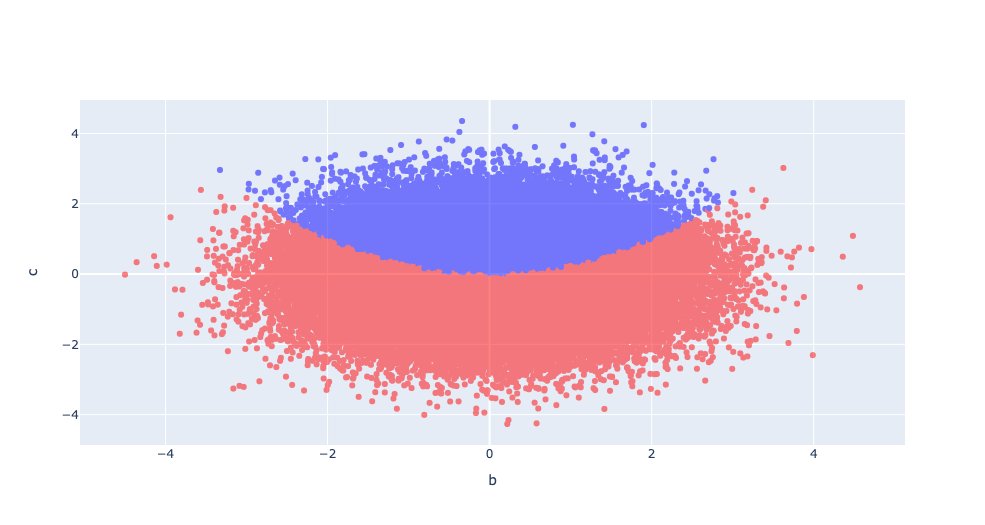
Let’s take a look at the discriminant when \(a = 1\). But let’s do this by graphing a whole ton of points and color coding the result for negative outcomes and positive outcomes. The image below gives a result for various choices of \(b\) and \(c\).
Ask your students these questions
- What do the blue dots mean?
- What do the reddish / salmon colored dots mean?
- What does the boundary between the blue and red dots mean? What is that function?
The blue dots represent the region where the discriminant is negative, the red where the discriminant is positive. The boundary is when then discriminant is zero.
Now if you are teaching a calculus or a probability class, you can convert this into questions about the likelihood of obtaining a quadratic with real solutions or complex solutions given some way of selecting \(b\) and \(c\).
Further extensions are to let \(a\) also be a free parameter. And now we have a 3D visualization exercise.
Reach out on Twitter or shoot me an email (mathmisery ~@~ gmail) or leave a comment if you want to chat more!