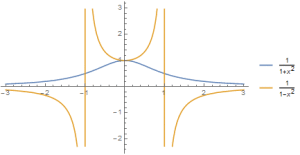
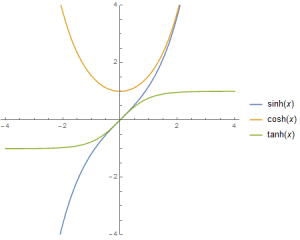Let’s look at two functions that my calculus book says are pretty different.
$$f(x)=\frac{1}{1-x^2}$$ and $$g(x)=\frac{1}{1+x^2}$$.
Their graphs sure look different, and finding antideriatives requires completely different techniques. For f(x), I’m supposed to use partial fractions:
$$\int \frac{dx}{1-x^2}= \int \frac{1}{2}(\frac{1}{1-x}+\frac{1}{1+x}) dx$$
$$= \frac{1}{2} (\log|1+x|-\log|1-x|).$$
On the other hand, g(x) requires a trigonometric substitution of x=tan t to give a very different-looking result.
$$\int\frac{dx}{1+x^2}= \int\frac{dt/\cos^2 t}{1+\tan^2 t} $$
$$=\int\frac{dt/\cos^2 t}{1/\cos^2 t}=\int dt=t=\arctan x.$$
We are of course exploiting a trigonometric identity here, $$1+\tan^2 t = 1/\cos^2 t$$ which is obtained by dividing the identity $$\sin^2 t +\cos^2 t = 1$$ by the square of cosine. (My calculus book also says I’m supposed to write ln for log, secant for the reciprocal of cosine, and stick a bunch of +C’s at the end of everything, but I’m a grown-
up and this is my post, so thppppt.)
Did the minus sign in the denominator really make these functions so different? After doing these two standard examples, students could easily be left with the impression that they are. They are not. Let’s integrate each of these functions using the “correct” method for the other function and see what my calculus book is not telling me.
First we will integrate f(x) with substitution. The sign is wrong to use the same trig identity as g(x), but not if we introduce the hyperbolic trig functions$$\sinh x = \frac{e^x-e^{-x}}{2},$$ $$\cosh x = \frac{e^x+e^{-x}}{2},$$ and $$\tanh x = \frac{\sinh x}{\cosh x}.$$
The following properties are easy to verify from the definitions.
$$\cosh^2 t – \sinh^2 t = 1$$
$$1-\tanh t = 1/\cosh^2 t $$
$$\frac{d}{dx}\cosh x = \sinh x$$
$$\frac{d}{dx}\sinh x = \cosh x$$
$$\frac{d}{dx}\tanh x = \frac{1}{\cosh^2 x}$$
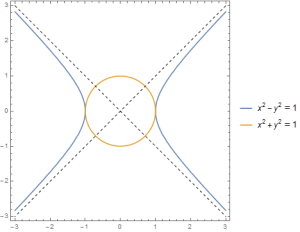
The first identity is worth a thought. Look at the curve x=cosh t, y=sinh t parameterizes: $$x^2-y^2=1.$$ The hyperbolic trig functions parameterize a hyperbola in exactly the same way the standard trig functions x=cos t, y=sin t parameterize a circle. Hence the name.
Anyway, that identity lets us integrate f(x) with the substitution x=tanh t. The calculation is nearly identical to how we did g(x).
$$\int\frac{dx}{1-x^2}= \int\frac{dt/\cosh^2 t}{1-\tanh^2 t} $$
$$=\int\frac{dt/\cosh^2 t}{1/\cosh^2 t}=\int dt=t=\mathrm{arctanh }\ x$$.
“But wait,” you say, “that’s not what we got before!” It is, because $$\mathrm{arctanh }x = \frac{1}{2} (\log|1+x|-\log|1-x|).$$ You can check that from the definition of hyperbolic tangent with some careful execution of logarithm and exponent rules, or you can simply note that by showing their derivatives are the same and observing that they agree at x=0, we just proved it using one of the most powerful techniques in mathematics: doing a problem two ways.
Now we will integrate g(x) with partial fractions. The obstruction seems to be that $$1+x^2$$ does not factor, but it does if we allow complex numbers. Those are numbers of the form a+bi where a and b are real and i is a magic new number with the property that $$i^2=-1.$$ In fact, every polynomial of degree n factors into exactly n linear terms with complex numbers. This is a property of the complex numbers called algebraic closure, and it is one of many reasons why complex numbers are in many ways more natural than real numbers. (Unfortunately, don’t hold your breath on modern high school curricula figuring that out.)
Here we go. You do need to trust me that calculus work just fine in the complex plane. You also need to trust me that it is alright to drop the absolute values inside the logarithm (defining the logarithm in the complex plane is actually a bit subtle because it really should take on multiple values, but trust me, this can all be sorted out).
$$\int \frac{dx}{1+x^2}= \int \frac{1}{2}(\frac{1}{1-i x}+\frac{1}{1+i x}) dx$$
$$= \frac{1}{2i} (\log(1+ix)-\log(1-ix))$$
$$= -\frac{i}{2} (\log(1+ix)-\log(1-ix)).$$
That last bit uses the handy identity 1/i = -i (to see that, multiply by i/i=1). Now we have some horrible mess with complex numbers all over the place, but we can get
rid of those fairly easily. First, remember the identity $$\mathrm{arctanh }\ x = \frac{1}{2} (\log|1+x|-\log|1-x|)$$ we proved above. This tells us that
$$\int \frac{dx}{1+x^2}= -\frac{i}{2} (\log(1+ix)-\log(1-ix)) = -i\ \mathrm{arctanh }\ ix.$$ What happens with those i’s now?
This gives me an opportunity to show off one of the most beautiful formulas in mathematics, $$e^{it}=\cos t+ i\sin t.$$ You can prove this with basic calculus using power series. You may have noticed that if you ignore the signs, the even coefficients of the exponential function are the terms of cosine and the odd terms are sine. The i‘s make the signs all match up. In real functions, exponential and trigonometric functions could not look more different. As complex functions, they are the same thing. In fact, the hyperbolic trig functions are the bridge between them:
$$\sinh ix = \frac{1}{2}(e^{i x}-e^{-i x}) = \frac{1}{2}(\cos x+ i\sin x – \cos(-x) -i\sin(-x))= i\sin x$$
Similar calculations give cosh ix = cos x and tanh ix = i tan x. From there, we can deal with our arctanh problem: if y=arctanh ix, then tanh y =ix, so x=-i tanh y=-tanh iy. Finally, -arctanh x =iy and so y = i arctanh x. We are using 1/i=-1 and that tanh is odd. We have now shown
$$\int \frac{dx}{1+x^2} = -i\ \mathrm{arctanh }\ ix=-i\times i\ \mathrm{arctan }\ x=\mathrm{arctan }\ x$$ with partial fractions.
A few pedagogical take-aways here:
- Some may complain that arctanh is unfamiliar and they’d prefer $$\frac{1}{2} (\log|1+x|-\log|1-x|)$$ because it just has logarithms. But once you spend five minutes looking at tanh x, you see it is an entirely reasonable function with easy-to-prove properties. I see arctanh x and I understand it completely because I can flip the graph of tanh x and see everything I need. When I see the logarithm expression, I want to go home. Don’t blame hyperbolic arctangent just because it is not on your calculator.
- This is an example of how you can solve some problems in real functions by briefly visiting them in the complex plane.
- Seriously, the complex numbers are just beautiful. Lots of geometry and everything’s easier.
- Go easy on your calculus teacher if you feel cheated. I teach lots of calculus and don’t usually get far into this, and I care enough to write a big blog post about it. Calculus is packed with content, and you really need to go back and smell some of the roses you barreled past the first time.
(Edits: Took care of some typos and a touch of sloppiness. Thanks Manan and Erik for catching them.)