Many years ago, I asked these two problems to my Intermediate Algebra class in a lecture once.
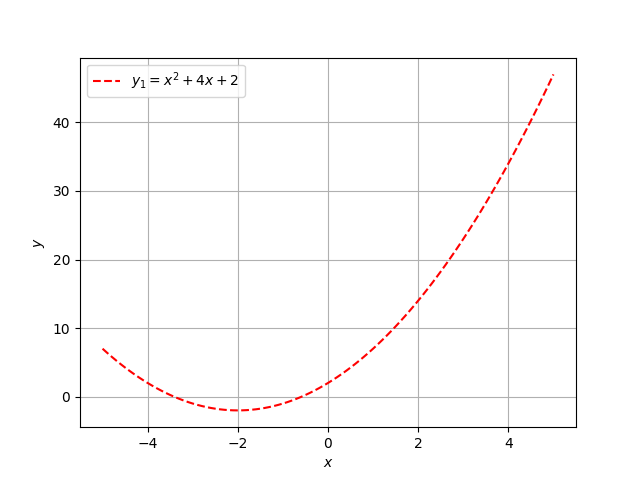
Problem 1
$$\mbox{Find all }x \mbox{ that satisfy } x^2 + 4x + 2 = 0$$
and I gave the following graph
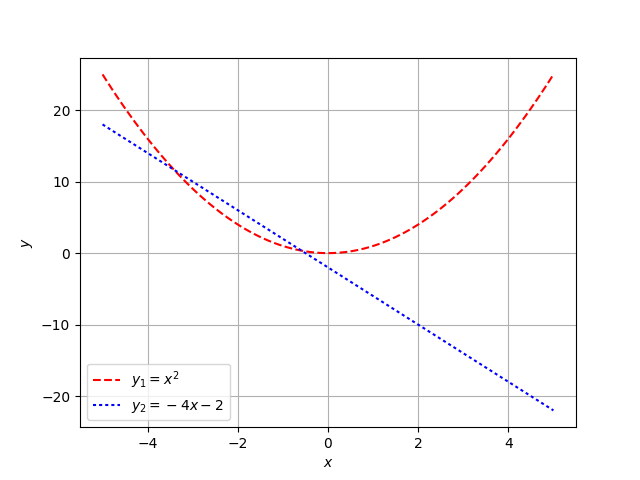
Problem 2
$$\mbox{Find the intersection of the parabola } y_{1} = x^2 \mbox{ and the line } y_{2} = -4x – 2$$
and I gave the following graph
Of course, you can probably guess as to what happened. Problem #1 had a higher success rate than Problem #2. This was done by design. We had just covered the many methods for finding roots of a quadratic and earlier in the semester we had gone over finding the intersection of two lines.
One thing that doesn’t get emphasized enough — and I think it would go a long way to clearing up a lot of little confusions about root finding — is how to look at quadratics. We had a nice discussion about Problem #2 above and how it is exactly the same as Problem #1. Students can understand the idea of “setting the equations equal to each other” when the equations are both linear. But, when one of the equations is \(x^{2}\) and the other a linear function, the idea of equating those two together doesn’t occur to them. This is forgivable and understandable in my eyes. If we only show to students the case of two linear functions being equated to each other, a broader general pattern may not get triggered. And this is why, Problem #2 is very useful — it expands on a technique they saw earlier in the course and becomes something they can extend.