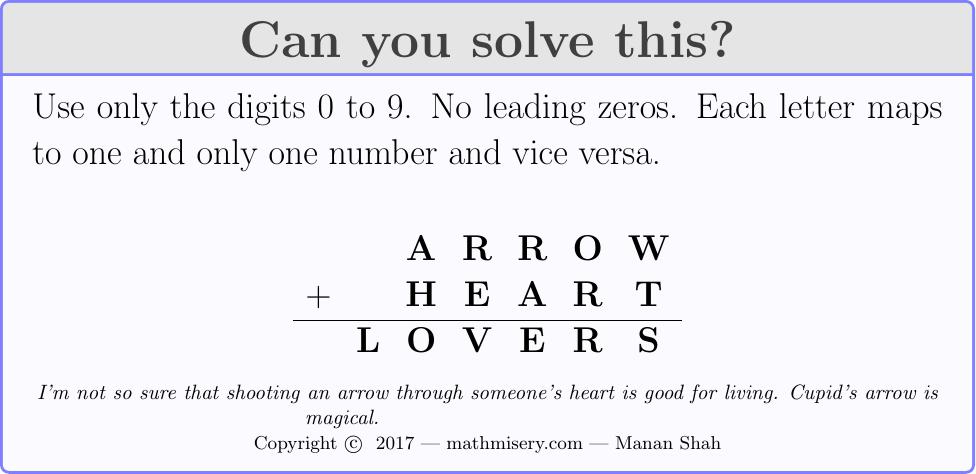I’m not so sure that shooting an arrow through someone’s heart is good for living. Cupid’s arrow is magical.
Were you able to figure out yesterday’s puzzle?
And here’s today’s puzzle! Leave a comment if you’ve solved it! Scroll down further if you want a hint [spoiler free].
Want a hint?