Converting from free to a paying subscriber is one of many challenges in SaaS product design. The idea behind the free tier in subscription-based products is to, among other things, create a large user base in a low-friction manner so that the product itself has life. Think: LinkedIn, YouTube, etc.
Another reason is to allow the user to experience the (near full) capabilities of the product and then to eventually bring them into a paying tier where various restrictions in the free tier are lifted. Some examples are “number of saves”, “number of teammates (aka seats)”, “storage capacity (in GB)”, “bandwidth”, “export options”, “number of design elements”, etc.
From a product and business analytics perspective, a task is to understand factors for conversion. A question template can be something like this: How many <X> within the first 24 hours, 7 days, 30 days, before they convert? Where <X> can be:
- unique features does a user interact
- times does a user log in
- saves
- unique actions does a user take
From here the rabbit hole of questions begin: “which features?”, “what order of features?”, “does time of day / which day matter?”, “is conversion associated with the user acquisition channel?”, “what type of content?”, “which user demographics convert best?” and so on.
Before going down all of this, there are some axioms worth thinking about. It feels like common sense that the more a user engages with the product, the more likely they are to convert. Hard to argue against this, however …
We know from either our own personal use of products or other common sense that more usage doesn’t mean more likely to convert. Some examples: if we want to “convert” our health from our current state to better, then it would seem physical exercise is necessary. But we know, obviously, that 24/7 physical exertion leads to death. There’s only so much sugar that we can have before we start feeling ill. Same for water.
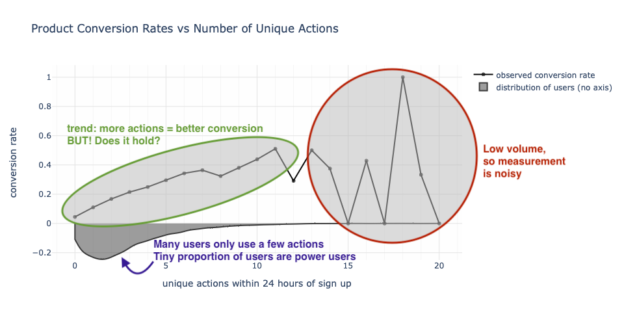
If we don’t like the examples that interact with the (bio-) physical world, then consider digital products that let us watch videos, make slideshows, edit images, talk to the chat AI, etc. for “free” (yes, yes, nothing is free because if you’re not paying for the product, you are the product or you are implicitly paying by watching ads). If we start to examine the data between product utility and conversion we may see a chart like the one below showing that as the number of unique actions taken increases so does conversion. But after a certain point (around 11 or 12 actions), the metrics are noisy because of low volume.
At this point, a mental bifurcation begins to take place. Our axioms aren’t being challenged as we see that the more unique actions a user takes, the more likely they are to convert. But beyond, say, 11 unique actions, the trend doesn’t seem to hold. It’s easy to hand wave this away by saying that there are not enough users, the measurement error is high, and there is nothing to really challenge the narrative.
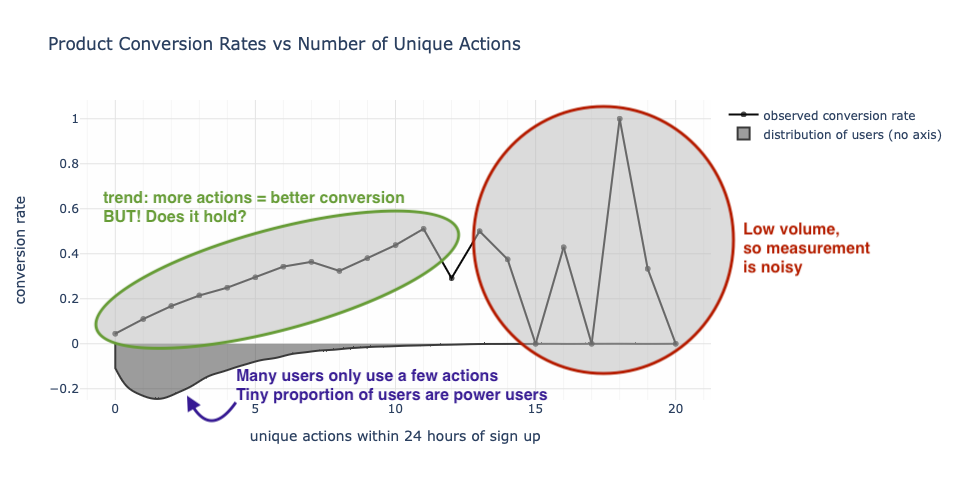
From a data modeling perspective, we may fit a logistic regression to this and get a graph that agrees with where the mass of the data exists as it continues the trend forward.
Since beyond 11 unique actions, there is low volume, we’re not particularly put off by the visual discrepancy between what’s observed and what’s modeled, especially because of that 100% conversion rate at 18 unique actions (modeled at 80%). Or maybe you are put off by the low conversion rates between 12 and 17 unique actions! In either case, not volume is low.
Reality may be more paradoxical and may require better product context. Is it possible that those “power users” they are actually getting a lower quality of experience because they are fumbling around on the product or that they have overused it? Is there a certain population of users who will just never convert because they actually have everything they need in the free offering? Or could we be in an uncanny valley where a certain set of users actually want even more things free before they convert? It could be all of the above.
Now we can also say “hey, who cares, this is such a small proportion of users that we are basically chasing data ghosts”. Possibly true. But the narrative of more action means better conversion is one of many that informs product strategy, product design, product pricing, etc. As we go from a few hundred thousand users to millions to tens of millions, we’ll start to feel the conversion realities in nominal dollar terms. Do we need to cram more things into the free offering or is there a limit?
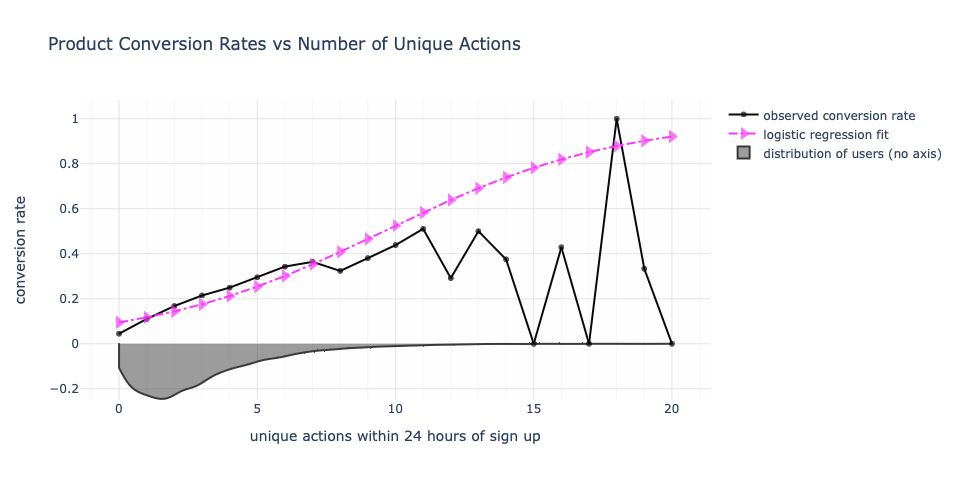
If we open ourselves to the possibility that there is a saturation point and add into the modeling the possibility of conversion degradation, then we a dissonant reality unfold. Under this new model, optimal conversion is somewhere between 9 to 12 unique actions. Beyond 12 unique actions, conversion starts to drop. A user taking 20 unique actions has a modeled probability of conversion equal to that of a user taking 3 or 4 unique actions in this new viewpoint. Whereas under classical logistic regression, they would be modeled to convert at 90%.
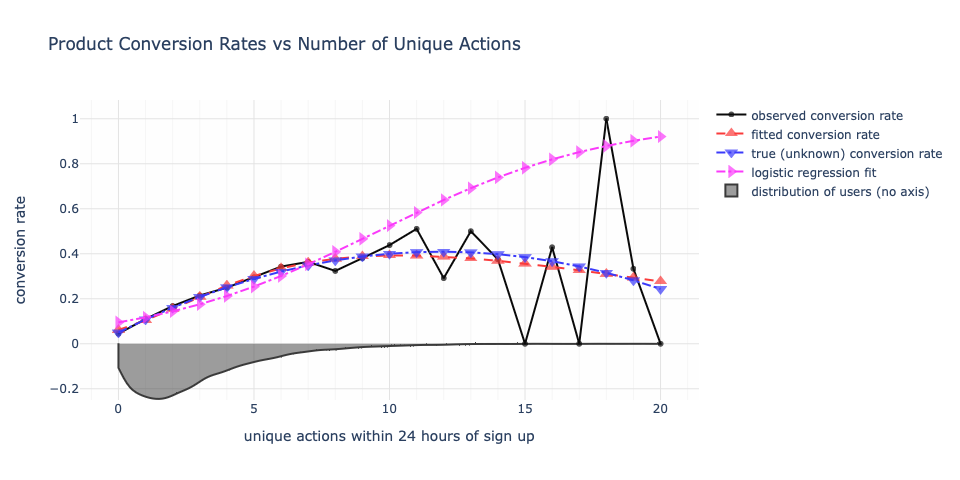
The true conversion rate is never known, but because this is hypothetical data, I do know it. The data model for regression does not have access to the true probabilities. It only has access to the observed data. The parametric form chosen is essentially logistic regression but with an additional exponential decay factor added in. If that decay factor were unnecessary, we would have obtained a weight of zero for that term and would have had the original logistic regression. But this was not the case.
Everyone and their cat will have an opinion on how to model this, but the point ultimately is on the parametric and axiomatic assumption that more actions means better conversion. This narrative if accepted as a point of fact influences the modeling assumption — that is, choosing a parametric model that is monotonically increasing in the number of actions.
We need to hold our narratives to statistical scrutiny.
Ideally, we want to “lift the curve”. Can we simply get a higher conversion rate on 1 unique action than what we have now? And this is a different conversation and a more meaningful use of product thought energy than always trying to push more engagement.