First, let’s do something “fun”. Take a look at this:

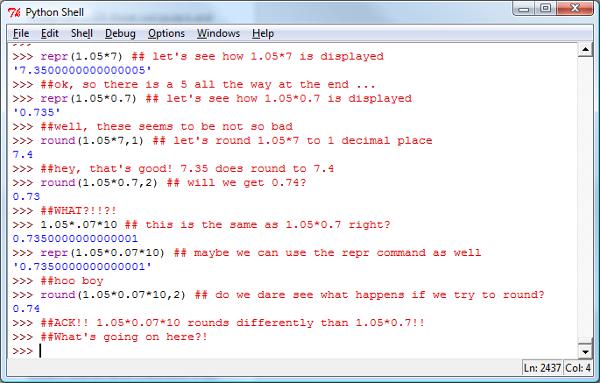
Numbers don’t work the way we’d want them to in a computer (“The numbers are in the computer?” Sorry, couldn’t resist.).

Broadly speaking, due to the finite amount of memory available, there is only so much precision that we can have. As a result, we can get behavior like the above.

So how are these numbers stored? Well, wikipedia seems to have a decent write-up.

As such, we’re not going to discuss IEEE standards today! We’re going to delve a little bit into Python’s \(\mbox{ as_integer_ratio }\) method for floats.

Here’s what Python’s (v 3.1.x) says:

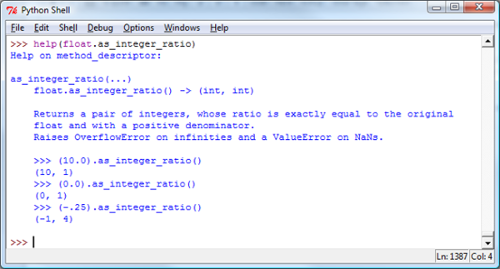
That looks good, right? We have a simple way to get the fraction representation of a floating point number via \(\mbox{ as_integer_ratio}\).

So let’s see what happens when we try a few numbers:

>>> 0.33.as_integer_ratio()
(5944751508129055, 18014398509481984)
>>> 0.45.as_integer_ratio()
(8106479329266893, 18014398509481984)
>>> 0.023.as_integer_ratio()
(3314649325744685, 144115188075855872)

So what happened? Why didn’t we get \((33,100)\) for \(0.33\)? It’s pretty much for the same reason that the \(\mbox{ round }\) method behaved the way it did. It’s not a problem with the method, it’s really just how these numbers are stored. Computers can’t store numbers like \(0.33\) exactly.

The computer is limited to adding in negative powers of 2. Thus the computer approaches \(0.33\) as follows:

• 0.25
• 0.3125
• 0.328125
• 0.3291015625
• 0.32958984375
• 0.329833984375
• 0.3299560546875
• 0.329986572265625
• 0.32999420166015625
• 0.3299980163574219
• 0.3299999237060547
• 0.32999998331069946
• 0.32999999821186066
• 0.32999999914318323
• 0.3299999996088445
• 0.32999999984167516
• 0.3299999999580905
• 0.3299999999871943
• 0.32999999999447027
• 0.32999999999810825
• 0.32999999999992724
• 0.3299999999999841
• 0.3299999999999983
• 0.3299999999999992
• 0.3299999999999996
• 0.32999999999999985
• 0.32999999999999996
• 0.33

Notice, that the last entry is \(0.33\). This does not mean that the computer got it exactly, it’s just that whatever number it has stored is indistinguishable from \(0.33\). Additionally, the display to the screen is calibrated to show \(0.33\). Really, the calculation is as given below.

$$\frac{1}{2^{2}} + \frac{1}{2^{4}} + \frac{1}{2^{6}} + \frac{1}{2^{10}} + \frac{1}{2^{11}} + \frac{1}{2^{12}} + \frac{1}{2^{13}} + \frac{1}{2^{15}} + \frac{1}{2^{17}} + \frac{1}{2^{18}} + \frac{1}{2^{19}} + \frac{1}{2^{24}} + \frac{1}{2^{26}}$$ $$+ \frac{1}{2^{30}} + \frac{1}{2^{31}} + \frac{1}{2^{32}} + \frac{1}{2^{33}} + \frac{1}{2^{35}} + \frac{1}{2^{37}}$$ $$+ \frac{1}{2^{38}} + \frac{1}{2^{39}} + \frac{1}{2^{44}} + \frac{1}{2^{46}} + \frac{1}{2^{50}} + \frac{1}{2^{51}} + \frac{1}{2^{52}} + \frac{1}{2^{53}} + \frac{1}{2^{54}} = \frac{5944751508129055}{18014398509481984}$$

If we use higher precision arithmetic, then $$\frac{5944751508129055}{18014398509481984} = 0.3300000000000000155431223448$$

Notice that to sixteen places this number matches up to \(0.33\). That’s all the precision that Python floats have (read the IEEE page cited earlier).

So what happened with our multiplication of \(1.05*.7\)? Well, \(0.735\) is stored as:

• 0.5
• 0.625
• 0.6875
• 0.71875
• 0.734375
• 0.73486328125
• 0.7349853515625
• 0.7349929809570312
• 0.7349967956542969
• 0.7349987030029297
• 0.7349996566772461
• 0.7349998950958252
• 0.73499995470047
• 0.7349999845027924
• 0.7349999994039536
• 0.7349999998696148
• 0.7349999999860302
• 0.7349999999933061
• 0.7349999999969441
• 0.7349999999987631
• 0.7349999999996726
• 0.7349999999999
• 0.7349999999999568
• 0.7349999999999852
• 0.7349999999999994
• 0.7349999999999999
• 0.735

$$\frac{1}{2^{1}} + \frac{1}{2^{3}} + \frac{1}{2^{4}} + \frac{1}{2^{5}} + \frac{1}{2^{6}} + \frac{1}{2^{11}} + \frac{1}{2^{13}} + \frac{1}{2^{17}} + \frac{1}{2^{18}} + \frac{1}{2^{19}} + \frac{1}{2^{20}} + \frac{1}{2^{22}} + \frac{1}{2^{24}} + \frac{1}{2^{25}} + \frac{1}{2^{26}}$$ $$+ \frac{1}{2^{31}} + \frac{1}{2^{33}} + \frac{1}{2^{37}} + \frac{1}{2^{38}}$$ $$+ \frac{1}{2^{39}} + \frac{1}{2^{40}} + \frac{1}{2^{42}} + \frac{1}{2^{44}} + \frac{1}{2^{45}} + \frac{1}{2^{46}} + \frac{1}{2^{51}} + \frac{1}{2^{53}} = \frac{6620291452234629}{9007199254740992}$$

And using higher precision arithmetic, $$\frac{6620291452234629}{9007199254740992} = 0.7349999999999999866773237045$$

This isn’t the whole story, though. There are a lot more shenanigans going on here. Multiplying finite precision numbers leads to a cascade of rounding and truncation errors. If done enough times, the errors can propagate so that you will have zero places of accuracy!

So, ye be warned, numbers are not what they seem.