I recently got to the part of my calculus class where I get to gleefully skip the section on related rates. I love skipping it. I get to feel like a real professor making real pedagogical decisions, and I earn some good will from the students who know what I just spared them from.
A related rate problem establishes two functions that depend on a single variable, usually time, where the functions are related by some governing equation. This equation is either explicitly given or is determined from the physics or the geometry of the problem. The rate at some time is given for one of the functions (i.e., you are given the derivative of one of the functions at a point). You are asked to find the rate of change of the other function at that time. This is possible by differentiating the governing formula implicitly.
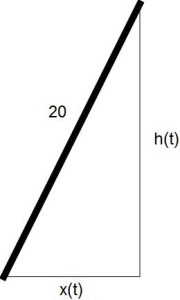
Here is a standard one: The top of a 20-foot ladder is sliding down a wall at a rate of 2 feet per second. How fast is the bottom of the ladder moving away from the wall when the top is 16 feet from the floor?
Let h(t) be the height of the ladder at time t and let x(t) be its distance from the floor. We suppress the t since we are never going to need to find its value (an important conceptual obstacle for many students, I think, is where the t is in all of this). By the Pythagorean Theorem, $$x^2+h^2 = 400.$$ Since this is about rates, we differentiate implicitly to get 2xx’+2hh’=0, or xx’+hh’=0. We are interested in x’ when h=16. We are already told h’=-2 (assuming the negative direction is downward). That just leaves x, which our Pythagorean relation shows must be 12. So 2xx’+2hh’= 2(12)x’+(16)(-2)=0, or x’ = 4/3 feet per second.
Here are some reasons I don’t cover this.
The material is terminal. Nothing in a typical calculus sequence depends on related rates. That’s not a complaint — there are plenty of good terminal topics in calculus — but it means the topic is eligible for skipping since it won’t screw something up down the road.
It does not fit in the narrative. Every course is telling some kind of story. Related rates are that unneccessary expository character that a better writer wouldn’t need to introduce. Maybe there is a perception that related rates make calculus feel more useful, but if you are having trouble selling calculus as useful then you just aren’t trying. Related rates have a completely different feel from anything else in the course.
It is a fake application. I get that we need to connect the material to the real world, but these are contrivances. Related rate problems never feel like something anyone would actually need to solve. This is in contrast to something like optimization where well-chosen problems can leave students thinking they may actually need calculus again some day.
There are only a few kinds of problems. This is a section where the strategy of trying one of each kind of problem and mimicking the right one can actually work. There’s the Triangles problem (e.g. slipping ladders, relative positions of vehicles, and lampost shadows; usually the governing equation is the Pythagorean Theorem, but they may use trigonometric relations if angles get involved), the changing volume or area problem (e.g. expanding oil slicks, melting snowballs, and inflating balloons), and the generic “here, just use this formula” problem (e.g., assorted physical laws, or an incredibly silly one I just saw quantifying two people’s love for one another. Their love is a conservative quantity for some reason. I’m not optimistic for this relationship.) .
It depends on a topic most students already find difficult. The rates being related concern implicit functions of time. Students in calculus often have a tenuous grasp of functions generally and implicit functions are hard enough on their own before piling story problems on top of them.
Many problems depend on other content. Many related rate problems require applying geometric formulas like the volume or surface area of the sphere or various physical laws. So now you have to wonder if a student missed a problem because she can’t do the calculus or because she just couldn’t remember that formula. Or you give the formula in the problem and you have telegraphed most of the solution. It’s awkward.
It reinforces mistaking answer acquisition for problem solving. This is the deal-breaker for me. Students can often navigate this section without actually learning anything because they can get by on mimicking examples. Every calculus teacher — every mathematics teacher — is perpetually battling this idea that if you can get the right answer then you understand it. If I am rewarding you for getting answers that you cannot explain outside of the limited context of a particular problem then I am not doing my job.
I’m not really this anti-related rate. I can see some non-standard calculus courses where the topic flows quite naturally. But with all of the content pressures on the standard curriculum, related rates just don’t fit for me. That’s one more day I could be spending on the Fundamental Theorem of Calculus.
Bill Wood is an Assistant Professor of Mathematics at the University of Northern Iowa. He tweets as @MathProfBill.
Pingback: Disintegration | Math Misery?
As a calculus student, related rates were the most interesting material of the entire year and the first time I actually felt like I had to actually plan out how to solve problems, even though it was extremely obvious once you got the knack for them.
That being said, related rates were on the AP calc exam when I took it, and I can’t imagine a credit for examination on calculus that wouldn’t include them. What curriculum demands are there for a high school course that is already beyond every state’s requirements? Unless by curriculum, you just meant, “content of calculus”.
My biggest worry is that by marginalizing related rates to your students, you are reinforcing the idea that “math is hard, esoteric, and so difficult that your teachers don’t want to do it so what hope do you have?” I’d sacrifice the goodwill earned over skipping the section by not discussing the difficulty of the section you are skipping.
*didn’t have the background that you were referring to college courses instead of high school. Apologies.
Related Rates is a good example in mathematics of where the name of the topic opens the door to understanding. The thrust of the technique is to develop a Relationship (an equation) between two or more Rates (derivatives with respect to t). In the process, we apply the idea of implicit differentiation, which is the Chain Rule. I don’t think of this topic as terminal as much as a capstone topic in a first semester calculus course, tying together a number of concepts and procedures, along with reinforcing ideas from geometry.
In theory, I don’t disagree. In practice, the way calculus is usually covered, I think the return on investment for this topic is very low.
I like to sell the Fundamental Theorem of Calculus as the capstone topic.
Funny you mention the marginal = derivative thing; although I also skip the economics applications section (it’s mostly just more optimization with extra terminology), I make that explicit point because I had a similar experience.
But everything in calculus has application in another field and we have to pick our battles. Even if we do value related rates as an application — and I don’t, because I think it’s a less useful topic than other things I also don’t have time to cover — most students get through it by parroting examples so they often don’t really learn it anyway. I suspect the student who sees it again in chemistry is better served with a deeper command of implicit functions and derivatives so they have the tools to build on those ideas when they appear in a context they care about.
Sorry, as one who taught calculus many times over 38 years as a faculty member, I can’t agree. While it is true that very little in the development of pure mathematics depends on related rates, the great majority of calculus students are majors in other fields. Applications of similar techniques in areas such as physics and chemistry abound. (There is even an intriguing example from astronomy found in a footnote to Fred Hoyle’s “The Black Cloud”.) Halfway through my own exposure to introductory economics, the coin dropped that “marginal” really meant “derivative of”, and I was severely annoyed with the professor that he hadn’t even alluded to the connection to calculus, if only for the benefit of a minority of students. There is also huge overlap in the ideas of modelling used in these problems and in optimization, including the identification of the meaningful domain of a problem. In fairness, it is hard to be completely convinced that the ideas are routinely transferred to courses in other fields, but failure to transfer is virtually guaranteed if mathematicians never address the essential ideas.