— attributed to Everett Dirksen
“Logarithm” is a big scary math word, and most people are comfortable dismissing logarithms to the realm of big scary math people. But “growth” and “scale” are not big scary concepts but are important in our everyday lives. Logarithms are essential to understanding them.
Cable news is filled with politicians and pundits with very strong opinions on economic policy, but they often demonstrate an understanding of the fundamental mathematics that would be laughable if it weren’t so terrifying. On a more personal level, many people’s lives would be radically different had they taken the time in their youths to understand compound interest. The banking industry relies on the fact that people do not.
The logarithm is a device for dealing with very large and very small scales and the exponential growth that moves us across these scales. Consider the function \(f(x)=\log_{10} (x)\). We may describe this function as “the power you need to put on 10 to get x.” So \(\log_{10} 10 =1, \log_{10} 1000 =3, \log_{10} 1000000000=9\), and so on. We can extend this idea to any positive number to say that the base 10 logarithm roughly reports the number of digits it has, minus one. I cannot calculate \(\log_{10} 123456\) in my head, but I know it is between 5 and 6, and closer to 5 than 6 because 123456 is closer to 100000 than one million. (It’s actually about 5.09.) Similar reasoning applies to very small scales where the exponents, and hence the logarithms, become negative.
A first step in comprehending the size of a number is to find how many digits it has, and that is just a logarithm. One spot of trouble is the graph. For example, in calculus I might want to draw \(y=\log_{e} x\) with a line tangent to the curve at, say, \(x=20\). (The logarithm with base \(e\approx 2.71\) is called the natural logarithm, often denoted \(\ln x\), and comes up everywhere in calculus. Calculus is also very concerned with finding the slopes of tangent lines, so this is a typical picture for any calculus class. Note also that changing the base does not qualitatively change the graph much because of the change of base formula.) We would probably draw something like the first picture (and this is also the picture that Wolfram Mathematica assumed I wanted when I plotted it):
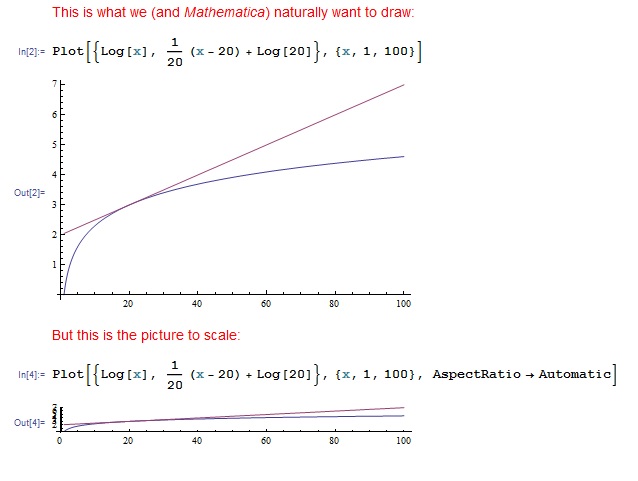
But the second picture is what the function really looks like, although for convenience we don’t often draw it that way. There’s nothing wrong with changing the scale of a picture, but if the whole purpose of the logarithm is to capture scale then we should make a big deal of it when we do! Students must recognize that the scale is such that the slope of that gently sloping line on the top picture is actually a minuscule \(\frac{1}{20}\).
Let’s put this another way, switching back to the common log \(f(x)=\log_{10} (x)\). Suppose a rabbit began moseying along a line at one foot per second when the Earth formed about 4.5 billion years ago. Meanwhile, a snail travels along the same line but is slowing so that the snail is at the base 10 logarithm of the rabbit’s distance traveled. The rabbit has managed to travel about \(1.4 \times 10^{17}\) feet since it started. That’s somewhere around the diameter of the galaxy. So in the time that it took the rabbit to stroll across the entire galaxy, how far did the snail get? Just over 17 feet. That’s really damn slow. Much slower than I’m sure many students realize after they leave the topic.
Logarithms are very slow-growing functions in exactly the same way that exponentials are very fast-growing functions. Exponential growth is everywhere and logarithms are essential to bring exponential growth to a manageable scale. These ideas appear in hands-on real-world issues like population growth and personal finance. Conversely, when we hear arguments that start sounding like the Dirksen quote above, we should look at tools like the logarithm to sort out the scale. Is a billion dollars a lot of money? It’s all relative.
Bill Wood is mathematics professor at the University of Northern Iowa. He tweets on mathematics and other matters as @MathProfBill.