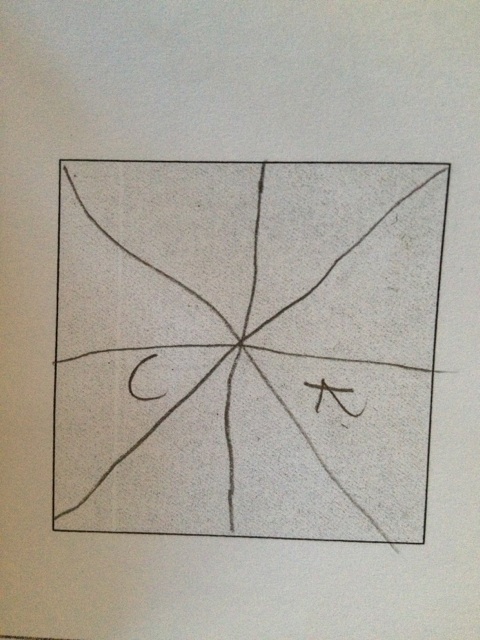
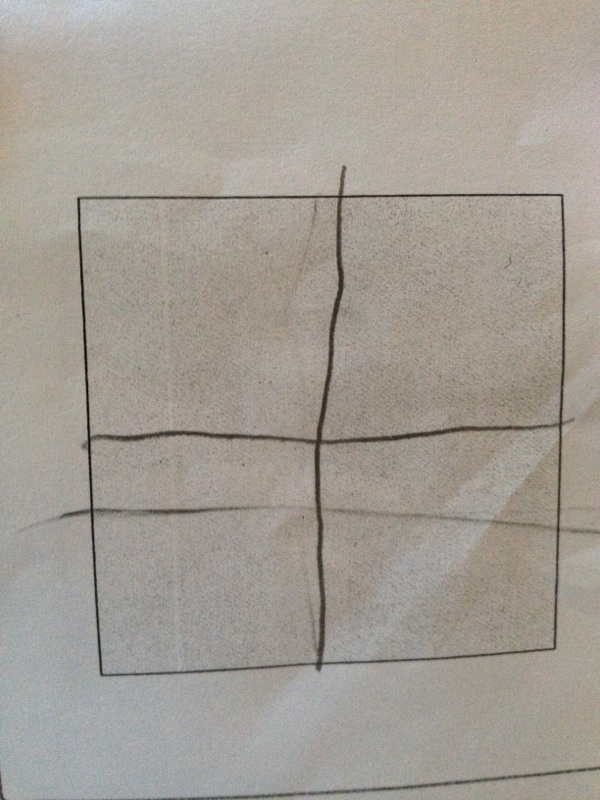
In yesterday’s article I left off with this image

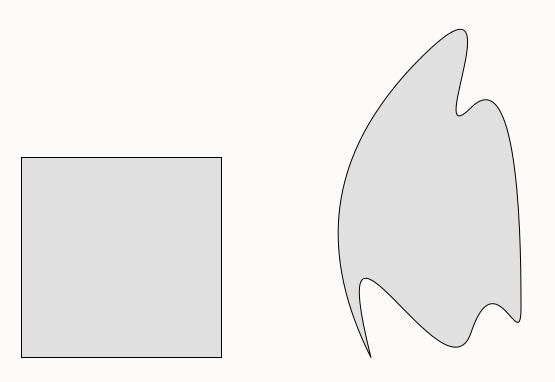
The Square

As we continued our pivot into sharing, we gave each pair of students [same pair from the arithmetic race] the square.

We asked them to share this square fairly between each other. There were no instructions beyond that. They could use whatever means they thought. We had anticipated that students would split this down the middle either by drawing a horizontal or vertical line roughly through one of the axes of symmetry. A diagonal slice was also one we thought we would see. Interestingly, we got more variety than we had anticipated.

Once they had completed their split, we asked them to explain why they split the square the way they did and if they both felt that the division was fair. All the groups agreed that the division was fair and generally said that each side got half. Getting half was fair and fair meant equal.

Here are some of the unanticipated divisions with commentary below each image.
They split it vertically down the middle, but then decided that a horizontal split was more fair. Why? The first time they split it, they eyeballed it. The second time, they used a ruler!

They imagined the square more like a window and used that as a model. Still, one person got one side of the window, the other person got the other side.

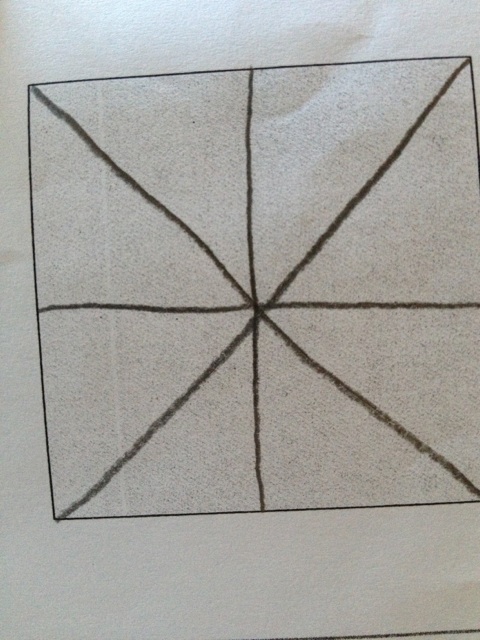It was more fair to make many splits than to make one split. But ultimately, they decided that one person would get the left half and the other person would get the right half.

The drew the first line and upon examination, decided it wasn’t fair. So they erased it and drew a new line. They both agreed that the new line was fair.

Another eight-way split.

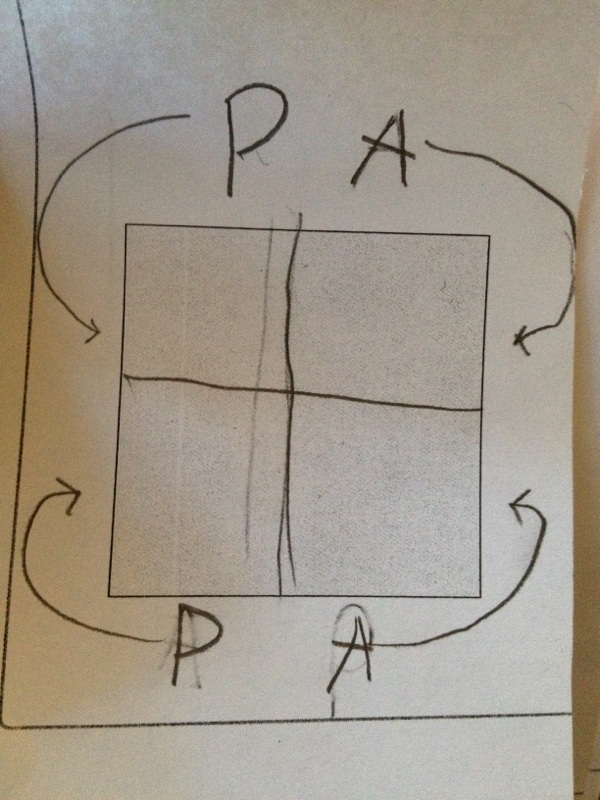They decided to quarter it and assign each of the quarters. They redid the vertical line split to a position which they both agreed was fair.

This was a pretty simple exercise. It was a warm-up and it was to get the students thinking about fairness and sharing. Now, we turned up the dial.

The Doodle

Next, we gave the second image, with the same instructions — share the doodle fairly with your partner.

Here’s what we got. These are all groups. I provide commentary below each image.

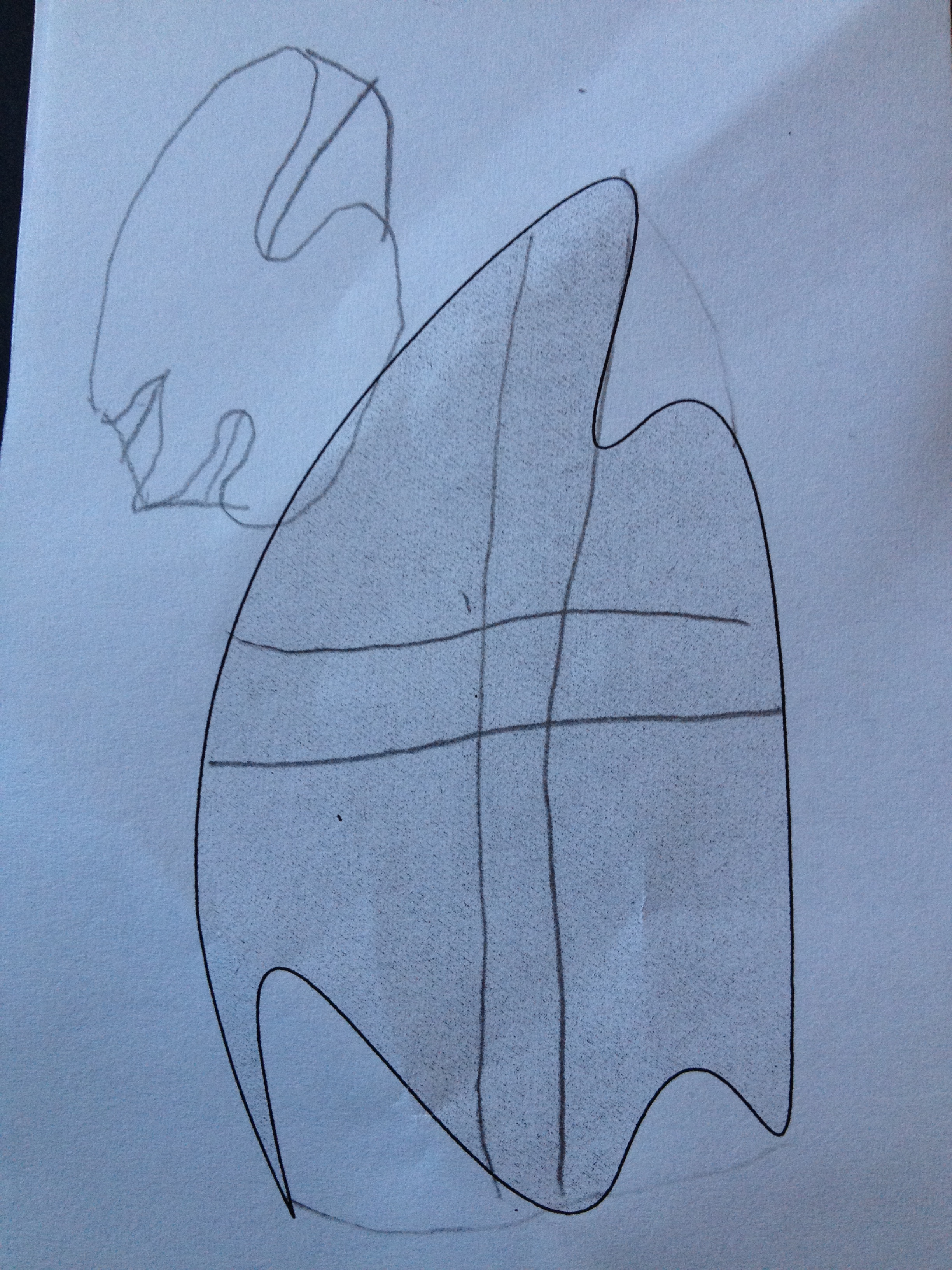They decided to “square” the doodle and identify fair division lines.

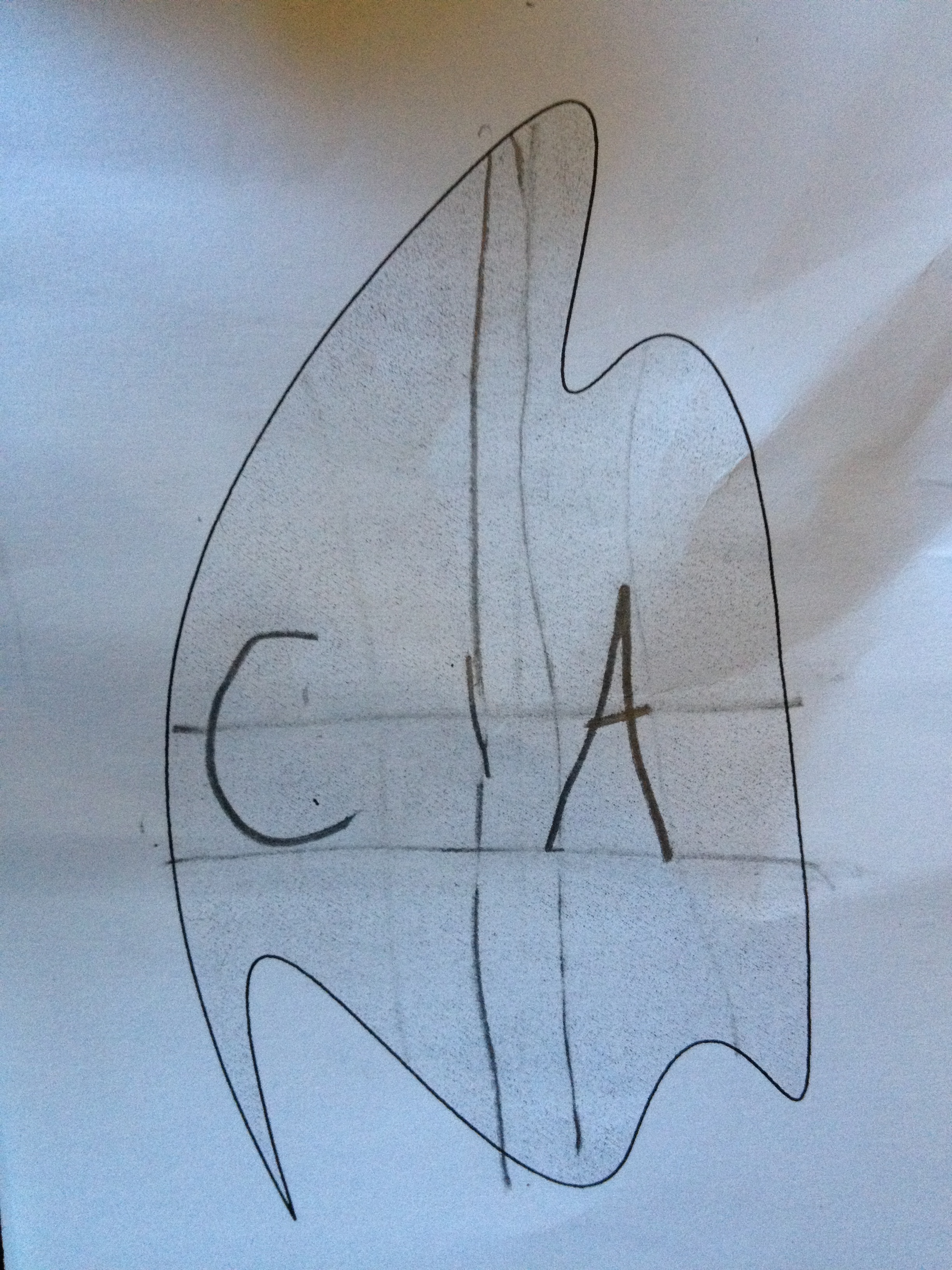They tried many iterations of lines until they could agree what was fair.

They divided the picture into four parts until each got two. They redrew the vertical lines, until they found a fair division point.

You will notice on the bottom right, there is a further minute subdivision, because this group divided it horizontally. They realized that one person would have gotten two humps and the other three humps, so they divided the small hump on the bottom right and gave one to each.

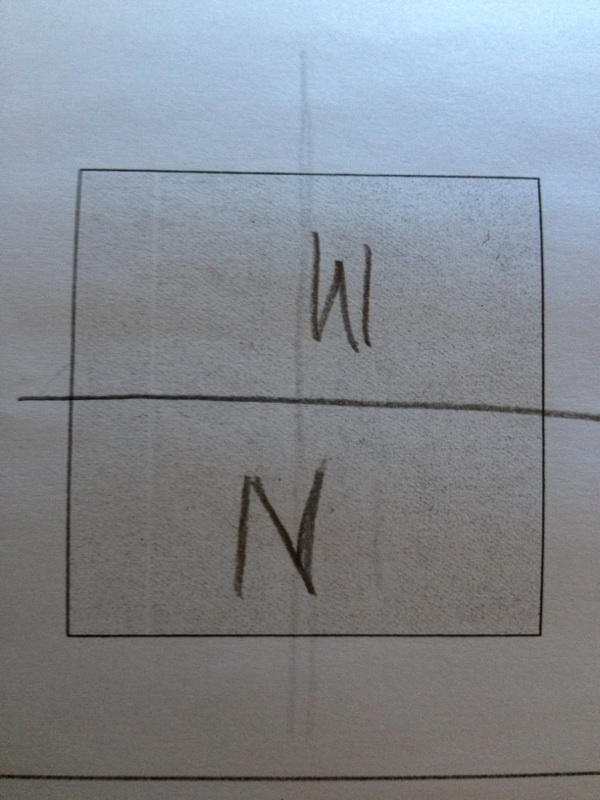
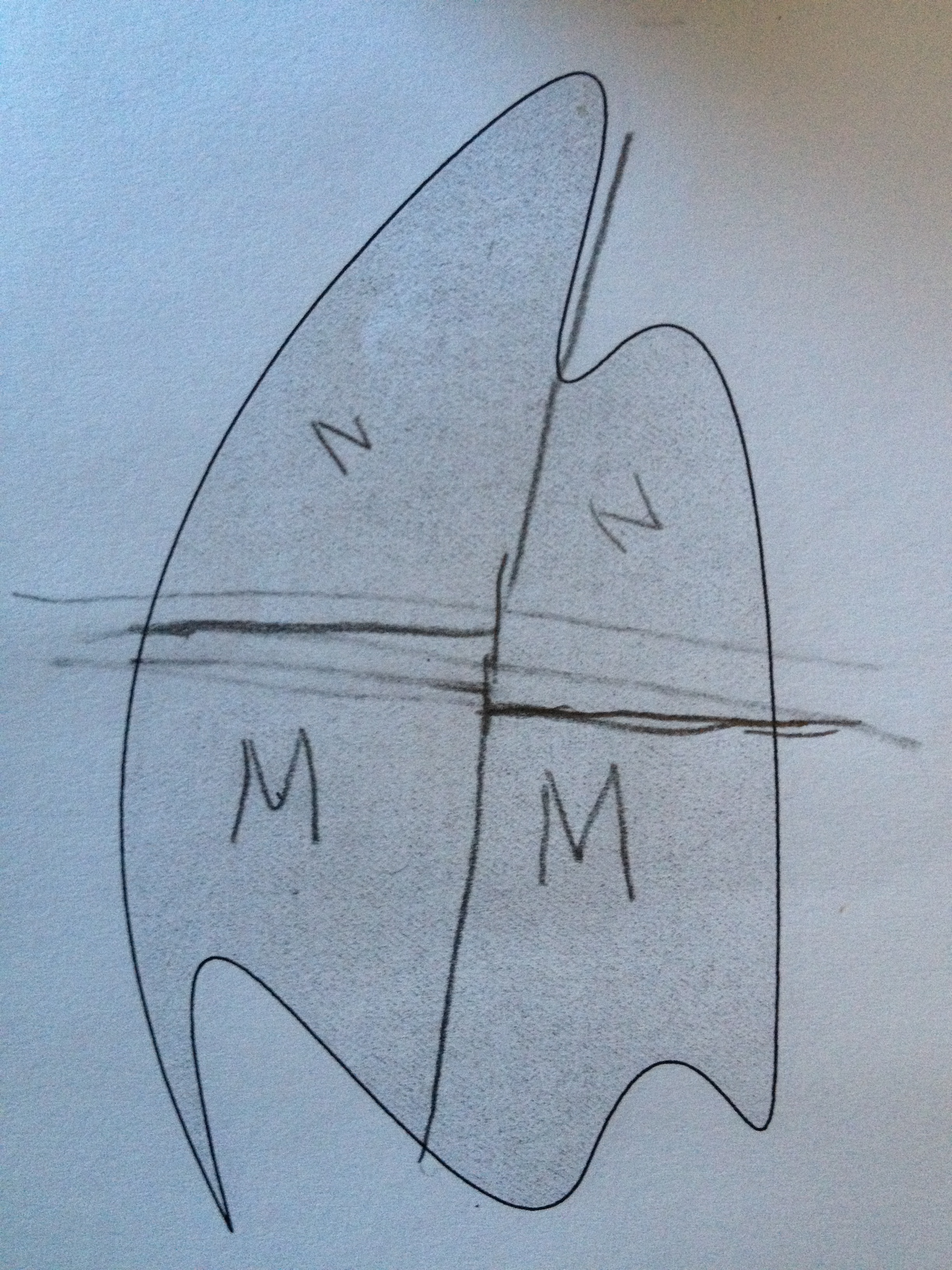They were happy at first with the initial line drawn [one of the erased ones], but then the idea that if this shape were a cookie, raised an objection with “N”. So, they brought a ruler and redivided it. After several iterations, they came to an agreement. “M” was reluctant to change because “M” knew that he/she had more. But, since they had to both agree on the division, they were able to come up with some measure of equity. Hence, the ruler came into play.

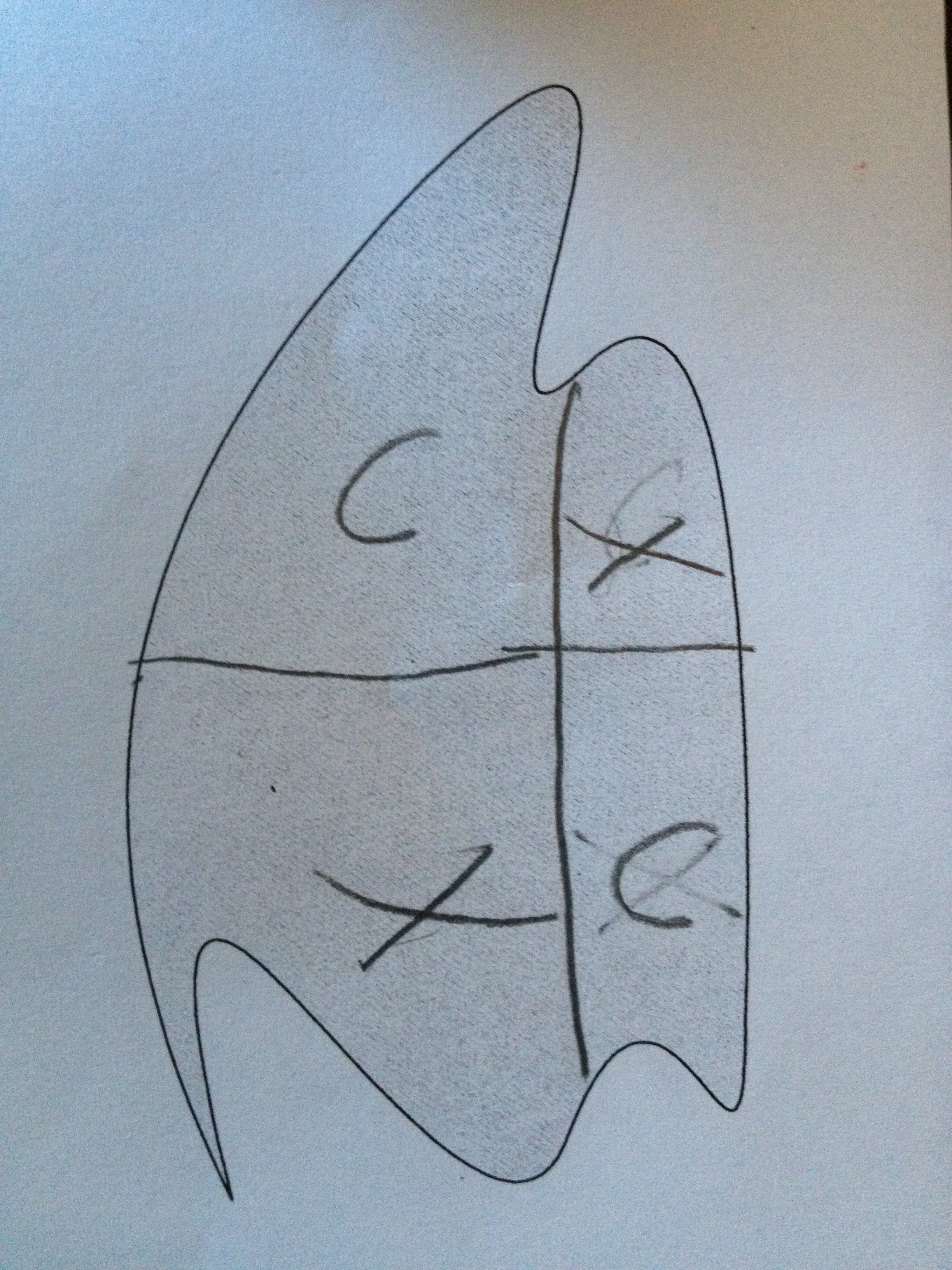They had initially sliced it horizontally in “half”. But then decided that it was uneven. So they sliced it vertically and gave themselves the same portions that they would have gotten with their original horizontal slice. Then, upon further thought, they realized that nothing had changed. So they swapped one of the quarters and felt that this was a fair division.

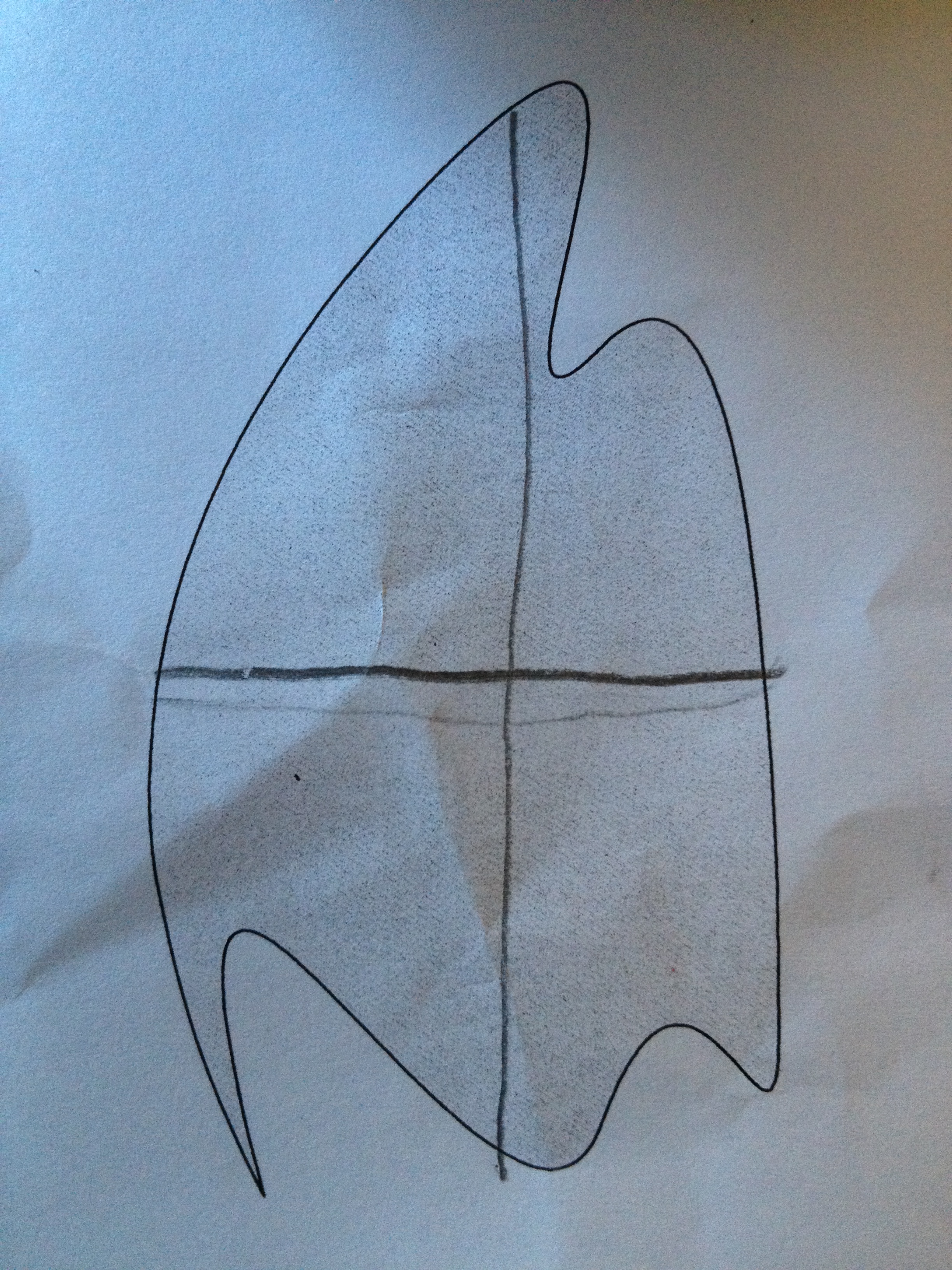They redrew the horizontal once and agreed to a split.

They split it horizontally, but didn’t agree on the split. So the split it vertically and didn’t agree and so decided to further split it. Despite this, one person got the top “half” [as indicated by the horizontal line], and the other person got the bottom half.

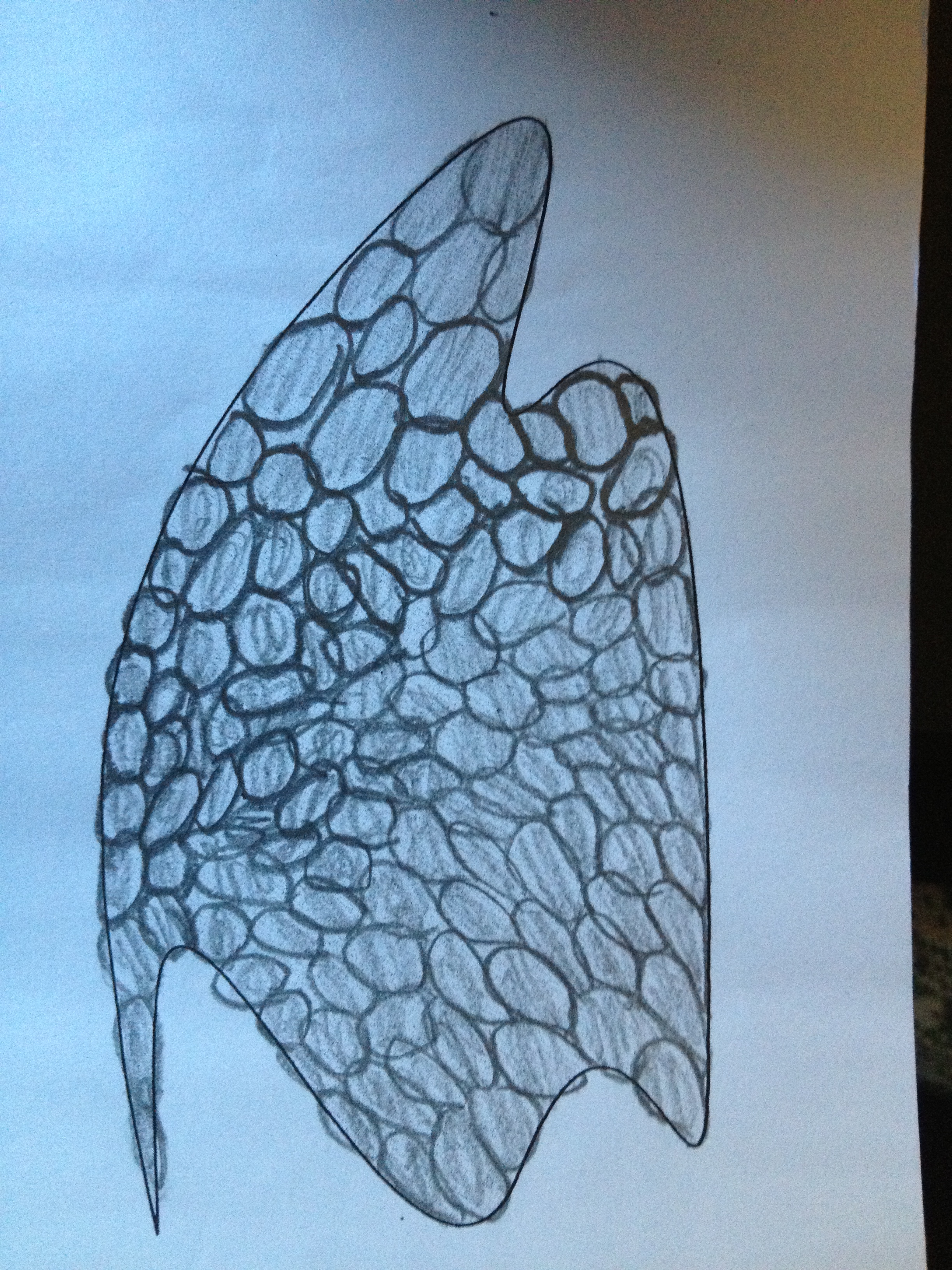Easily the most ingenious solution. They drew roughly similar sized ovals to tile the shape. They counted the ovals and realized had 127, so they adjusted it and made it so that there were 126 ovals and agreed that one person would get half, the other person would get the other half. A brilliant solution as it is a precursor to Calculus! They intuited the idea of area, decided to find a reasonably standardized way of tiling the shape, and made sure each side got an equal share by making sure there were an even number of ovals.

The students agreed that splitting this shape fairly was more difficult than the square. But ultimately, they were all able to come to some agreement. Next, we showed them a different way to split the shape in a way that we would both find fair.

Continue on to part 3. I leave you with this to ponder before you go on: we drew one line. What did we do? Also, we had some fun with Play-Doh!