Puzzle #1

You receive $1, $5, $10, $20 in that order until you have 2020 bills. How much money do you have?

Puzzle #2

Which has greater area: a circle with radius 20 or a square with side length 20?

Puzzle #3

Which has greater area to perimeter ratio: a circle with radius 20 or a square with side length 20? Can you generalize to circle with radius \(r\) vs square with side length \(r\)?

Puzzle #4

How many distinct four-“character” rearrangements are there of \(\{2,0,2,0\}\)? Note: 0022, for example, is allowed since I’m not asking for a four-digit integer.

Puzzle #5

How many distinct four-digit integers can be constructed using \(\{2,0,2,0\}\)?

Puzzle #6

How many distinct numbers can we make using \(\{2,0,2,0,.\}\)? For example, 0.022 and .0220 are the same number.

Puzzle #7

If you wrote all the integers in \([1,2020]\) as one string of digits, how long is this string? eg, \(1234567891011121314…20192020\)

Puzzle #8

Find the only non-zero, real solution to \(x^{20} – 20x = 0\)

Puzzle #9

From the previous problem, if \(v\) is the non-zero solution, then how many times does the sequence “20” show up in first 2020 digits of \(v\)?

Puzzle #10

Which is larger, \(2019^{2020}\) or \(2020^{2019}\)?

Puzzle #11

Consider a fair, 20-sided die where each side has a value between 1 to 20 on it and all values between 1 to 20 occur exactly once. If you roll this die 20 times, what’s the probability that the sum of all the rolls exceeds 200?

Puzzle #12

How many times, at minimum, do you need to flip a fair coin so that you have at least a 50% chance of observing 2020 heads?

Puzzle #13

Consider a normal distribution with mean = 20 and standard deviation = 20, or in formal math writing: \(Z \sim N(20,20)\). Find \(z\), such that \(F(Z < z) = 0.20\) to four decimal places of accuracy.

Puzzle #14

Find the fraction representation for \(0.\overline{2020}\) and compare this to \(0.\overline{2019}\)

Puzzle #15

Write 2020 as the sum of cubes of three integers, not necessarily distinct, if possible. Note: 2020 mod 9 is 4, so let that be a hint … 🙂

Puzzle #16

What is the smallest positive integer, \(n\), such \(2020^{n}\) has at least one copy of each digit in base 10?

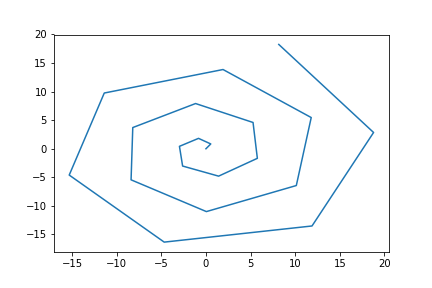
Puzzle #17

The spiral given in polar coordinates is \(r = \theta\) and when translated into Cartesian coordinates is given as \(x = r\cos(\theta), y = r\sin(\theta)\). What is the arc length of the curve in the \(x\)-\(y\) plane for integer \(\theta\), with \(0 \le \theta \le 20\)?

Puzzle #18

Find the largest integer \(N\) such that \(\sum_{i=1}^{N}i \le 2020\).

Puzzle #19

Both of these are incredibly difficult, but of these, which is more likely to occur. (A) A computer picks 20 integers, at random without replacement, between 1 and 80, inclusive and you do the same. What is the probability that you and the computer picked the same set of twenty numbers? Order doesn’t matter and you and the computer pick independently of each other. (B) A computer picks 20 integers, at random, between 1 and 20, without replacement. What is the probability that the computer chose all 20 numbers in numerical order [1, 2, 3, 4, …, 18, 19, 20]?

Puzzle #20

A clock with a minute and hour hand (do you all know what this device is?) reads 8:20 (20:20). What is the angle between the minute and hour hand?