Odds are you did raise your hand. Most high schools and now a growing number of primary schools offer or require students to take a second language. Typically, students will take three or four years of one of Spanish, German, French, Italian, or Latin in high school. Some schools offer Russian, Mandarin, or Hindi.
How many students come out fluent after years of foreign language study? YEARS. For all intents and purposes and speaking pseudo-statistically, that number is zero. If you are a foreign language teacher, you probably have a few counterexamples and I grant that. But, if we were to poll high school students who have taken three or four years of a foreign language and gauge their level of fluency, I would venture to guess that an overwhelming number will not be fluent. They may have decent reading knowledge or the ability to muddle through a restaurant menu at a fancy French restaurant, but practically none will be fluent.
The type of fluency I am talking about is conversational fluency in the same way that we would speak our native language. I do not mean legalistic fluency — that is, the ability to read through a legal document. Reading a legal document is, in my mind, one level of fluency above conversational fluency. As a fluent English speaker, I can listen to a news broadcast midway and understand what is being said, or I can comprehend part of an overheard conversation, or even glance quickly at a passing roadway sign and identify key words or phrases. Part of this ability is just an overfamiliarity with what to expect and there has been a decent amount of research that shows that we utilize an anticipatory process to understand / know what words or phrases are coming next. This is what makes up fluency.
Now, good students of foreign language study at the high school level will have a reasonable good vocabulary and good command of language structure and grammar. They may not necessarily know what the pluperfect is, but they will at least be able to speak in the past, present, and future. The average student will have a more limited vocabulary and have to think more readily about conjugations, cases, gender agreement, etc. than the good student. But every student will know the curse words: mierda, merde, Scheiße. The Spanish student, for example, may know and easily recall words like cajones, culo, penga, etc. The French student: “Voulez-vous coucher avec moi.” and maybe if they’re really feeling up to task, they’ll toss in a “ce soir” at the end.
But ultimately, fluency is non-present and this is after years of study. If I lived in Spain or Germany for one year, I’d come back fluent — hell, probably six months and I could probably cuss a whole lot better, too. So how is it that we have millions of students who take a foreign language for three or more years and at the end of all the conjugation drills and vocabulary tests and short essays and daily journals and reading Lorca or Sartre or for my college German class “Literatur Eins” that the level of language proficiency is generally worse than a three or four year old raised in that language? It’s a rhetorical question, but I’ll answer it anyway.
The problem is immersion, or rather, a lack of it. The problem isn’t the foreign language teachers. The problem isn’t even the curriculum at the content level. The problem isn’t worksheets or grammar drills or lack of engagement as some may argue. The problem simply is immersion and that’s an educational culture problem.
If we really wanted our students to learn a foreign language, we would require that they spend one or two years immersed in that environment. All subjects, all classes, homework, exams, etc would be in that language. And if I had to conjecture, we’d have students fluent in a second language. But we neither have the educational structure, human resources, nor the, if you will, cajones to do this.
What’s Your Point Shah?
I’m droning on about foreign language study and our inability to end up fluent because this is exactly the same problem, abstractly with math education. How the frack is it possible that students start working with fractions from the fourth grade or earlier and by the time they get to college they still have no smurfing idea how to work with them?
As much as we want to believe it’s an instructional issue, or a curriculum issue, or “context” issue, at the highest level it’s an immersion issue. Of course, there are instructional problems and curriculum design problems, but these take a back seat to the general problem that mathematics isn’t adequately immersed into a student’s education. I can similarly argue that every other subject isn’t adequately immersed into a student’s education.
Let’s think about this. If we wanted students to get a steady dose of mathematics or any subject, we would sprinkle those subjects through into all the other subjects. There’s nothing wrong with having dedicated time for mathematics or history or biology or Spanish. But when learning, say, mathematics, we can learn a little history or biology or Spanish, too.
Math education is often criticized for not having enough context, but I’ll criticize education in general the other way. Why don’t we talk more about mathematics in a history class? How many horsemen did Genghis Khan have? What does that imply for the amount of food they have to carry for the horsemen and the horses? And since the conquering Mongols often brought their families what does that imply in terms of overall food supply? What about the rate at which the whole camp moved? How much faster were the Mongol light cavalry units than, say, the Teutonic knights? What was it about the composite bow that made the Mongol horse archer so deadly? (Hey that’s physics!) And in this we’re getting an amazing history lesson not just about a particular time in history about the logistics of warfare, the various technologies that existed, the asymmetry in fighting styles, systems of organization (how did these older cultures / empires communicate over such vast distance when the fastest mode of travel was by horse!), etc.
Can we talk about mathematics in Spanish class? Absolutely. It’s a great way to build that vocabulary and to try to recommunicate some of those math facts and concepts in Spanish (some Spanish classes already do this). Conversely, we can talk about Spanish in math class. Math as it is taught in the US is not necessarily taught the same way in other countries. Take this Wikipedia article on long division. As language teachers will likely agree, learning a foreign language isn’t just about learning the language, it’s about learning the culture associated with it. And with a language like Spanish, there are many cultures. Why not have this little diversion into how division is taught in Latin America? From a math teacher’s standpoint it’ll likely help when trying to understand why some students can’t get help at home. It’s probably because their parents have never been taught math the way their kids are learning it in the US!
Can we talk about History and Biology? Absolutely. If we want to stick with the theme of warfare, well there’s the gory, gruesome biological warfare. And contrary to what some may think, biological warfare goes back millennia. Think, snake venom tipped arrows, plague rats, catapulting carcasses and fecal matter into a besieged city, etc. It’s ugly stuff. And that ancient biological warfare, just like modern biowarfare had a tendency to backfire. How many archers died from their poison arrows because they accidentally stabbed themselves? There’s also just the general biographies of the well-known scientists — that’s history, too.
Math and Biology? Easy-peasy. Bacteria growth is a classic example. Bulk flow is a good one for Calculus use. Brownian motion is some heavy math (Stochastic Calculus, which is much much later typically graduate level), but there’s nothing wrong with talking about it. Predator-prey models for differential equations. But even at a more basic level we have the mathematics of data science — actual measurement and statistical analysis.
But we don’t have this. Some schools do this. Some classroom teachers do this. Some institutes promote a cross-discipline interaction, but by and large, we don’t have this as part of general culture of education. What we have are discipline silos.
What do our students end up “knowing” after 10+ years of math education?
Nothing more than a few simple phrases and a bunch of curse words like these:
- Anything times one is itself.
- Anything times zero is zero.
- A negative times a negative is a positive.
- We always reduce fractions. (Why?)
- “… and then you carry the one …”
- You can’t divide by zero. (But this is “advanced” cursing. This eventually gets confused, anyway, so then the cursing becomes laughably stupid.)
- Cross multiply.
- \(a^{2} + b^{2} = c^{2}\) (And apparently it doesn’t matter if you have a right triangle or not, any time you have \(a^{2} + b^{2}\) it has to be \(c^{2}\) (a room full of math teachers proved this to me). Side story, at a conference talk I gave, I wrote on the board \(a^{2} + b^{2}\) and asked what it equaled. The room filled with math teachers said in unison \(c^{2}\), yet I had given no context of any sort. Fall backs on convention and reflex. Why couldn’t the right hand side have been 1? or \(z^{94}\)?)
- Negative “b” plus or minus the square root of “b” squared minus four “a” “c” divided by two “a”. Sometimes this is sung to Pop! Goes The Weasel.
- “You have to FOIL it.”
- SOHCAHTOA
- Sine cosine cosine sine, cosine cosine sine sine.
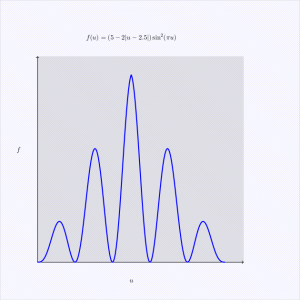
You know what I have to say to all this? \(f(u)\)! Where $$f(u) = (5-2|u-2.5|)\sin^{2}(\pi u)$$