If you happened to stumble upon this post, you may want to read part 1 and part 2 to get an idea of what this is all about.

We left off here:

The students agreed that splitting this shape fairly was more difficult than the square. But ultimately, they were all able to come to some agreement. Next, we showed them a different way to split the shape in a way that we would both find fair.

Tune in tomorrow for Part 3! In the meanwhile, I leave you with this: we drew one line. What did we do? Also, we had some fun with Play-Doh!

And here we are, at tomorrow and hence part 3.

Here’s our doodle. Now it was our turn to demonstrate fair sharing.

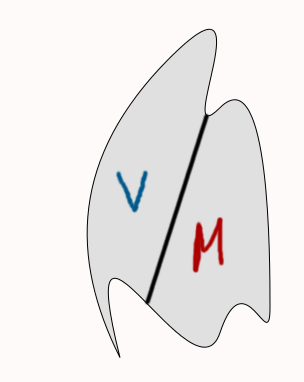
First we played a round of rock-paper-scissors. Mrs. Valentine won. What was the point? Well, we put the image on the projector and Mrs. Valentine drew a single line dividing the image into two separate regions. Then, I chose one of those regions and by force, Mrs. Valentine got the other region. The image below is a rendition of this. [I lost our version, so we re-did this on the computer for this article.]

Now, you may know what this method is called, but our students didn’t. Before we revealed what was so fascinating about this, we asked them if this split was fair. Half the students said that this wasn’t fair and the other half said it was fair. The “not fair” crowd said that I got three humps and Mrs. Valentine got two humps [so it was biased in my favor], or that Mrs. Valentine got the longer part [so it was biased in her favor], or that my piece had more [biased in my favor]. The “it is fair” crowd thought that both of us got the same amount.

After a few minutes of this, we explained that what we did was something called the “divider-chooser” method. The way it works is that one person divides and one person chooses. I gave them a different example why this was fair. I reverted back to the square and gave the process:

I am going to cut this square and Mrs. Valentine will pick the part that she wants.

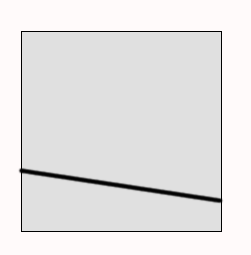
Next, I drew the cut as shown in the image below and asked them, does it make sense for me to divide the square like this?

Unanimously and in unison they declared “NO! Mrs. Valentine would get the biggest piece!” And there we had it — a moment of clarity. They understood that if one person has to divide it and the other person chooses, then the divider would never want to slice it in such a way that would result in them getting the smaller piece, or more abstractly, an unfair share.

We asked them why the divider couldn’t also choose first. They thought about this for a little bit until someone said “because you would always give yourself the biggest piece”. The other students nodded. It made sense — selfishness always makes sense once we can see the path to it.

We also noted that we did rock-paper-scissors to decide who would be the divider. We thought that was a fair way to do it.

Now, it was their turn. We gave them the doodle again and asked them to split it into fair shares by electing a divider [and hence a chooser]. Here’s what we got. My commentary follows each image.

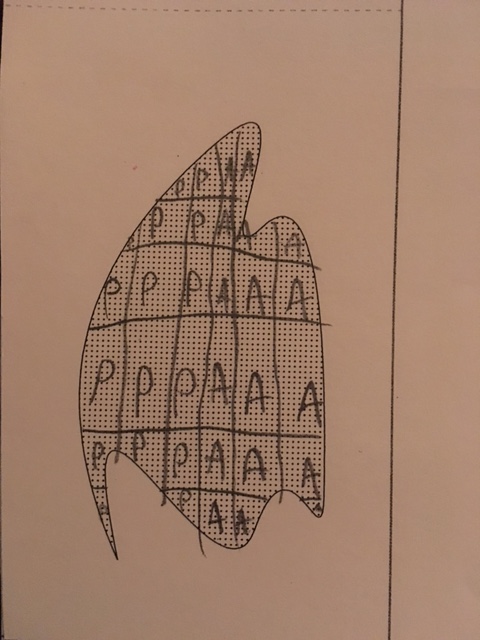
The divider couldn’t find one spot to split the shape, so they drew several dividing points and the chooser got to choose all of them! This method is not fair, but neither realized this and “A” chose the right and “P” chose left. Amusing! The thought was there maybe in mimicry but it’s not clear if the idea made it through.

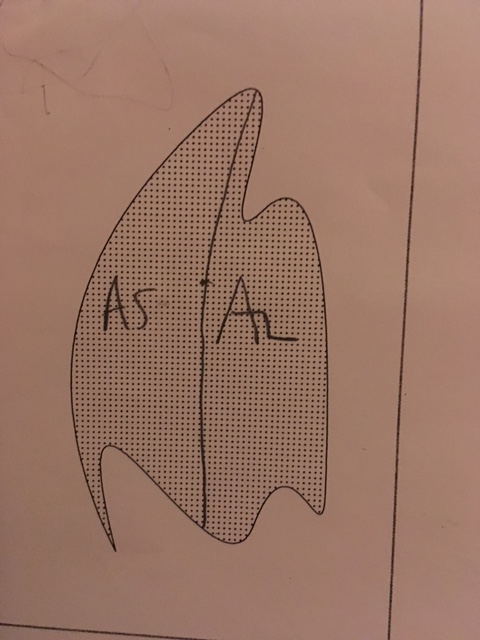
This is not a bad split. It looks approximately equal.

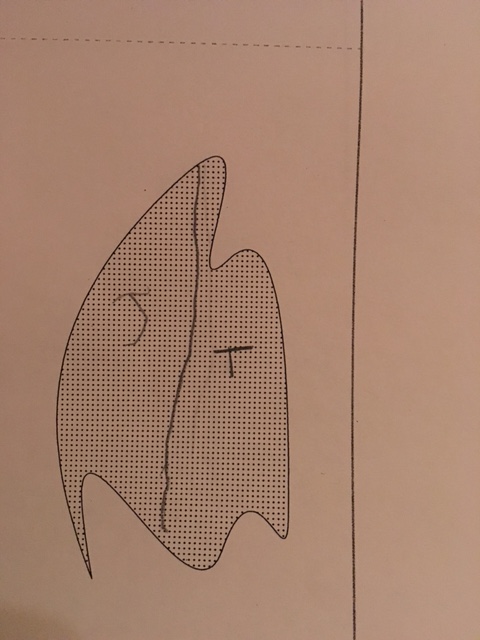
This is another similar, single line split. Not bad!

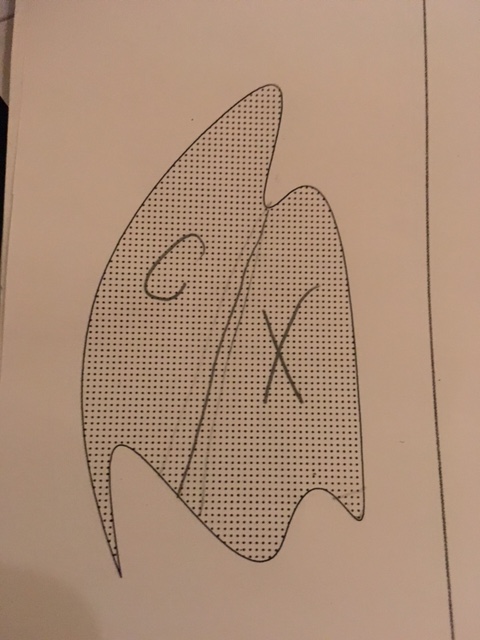
The divider took a few tries and eventually found a spot that felt fair enough to let the chooser choose.

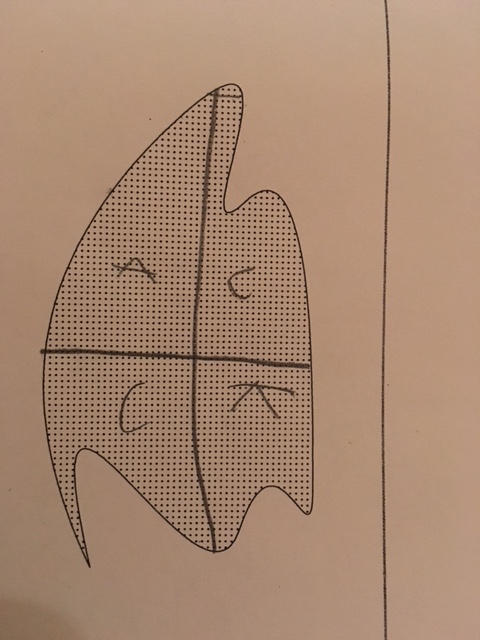
Ah, another similar multi-line split. This is biased in favor of the chooser, but eyeballing it, it looks like they got things balanced.

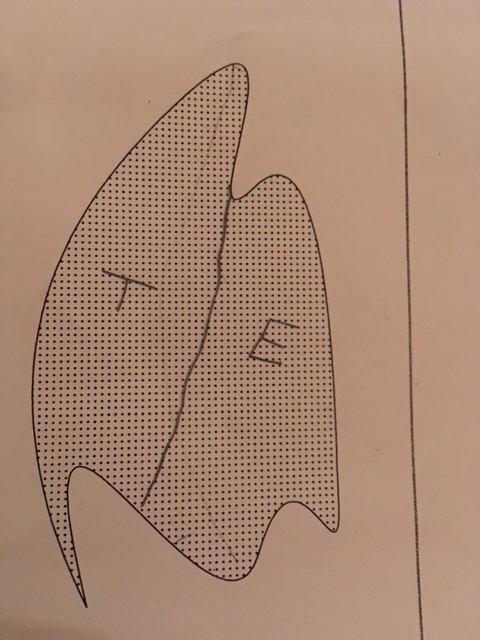
A split that was similar to the one Mrs. Valentine made. Mimicry at its finest.

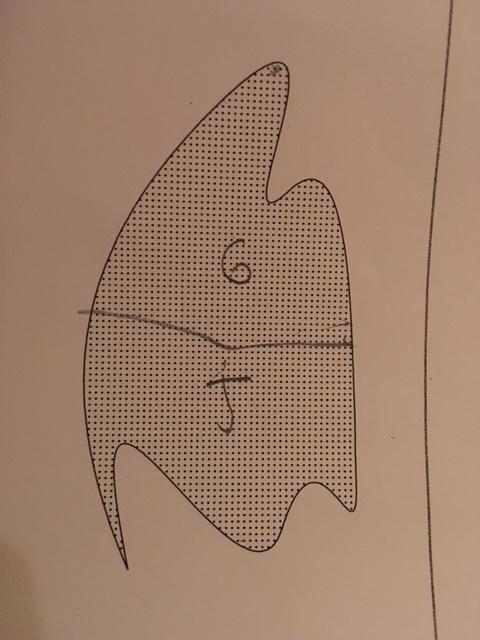
This is a nice horizontal split and both “G” and “J” were happy with it.

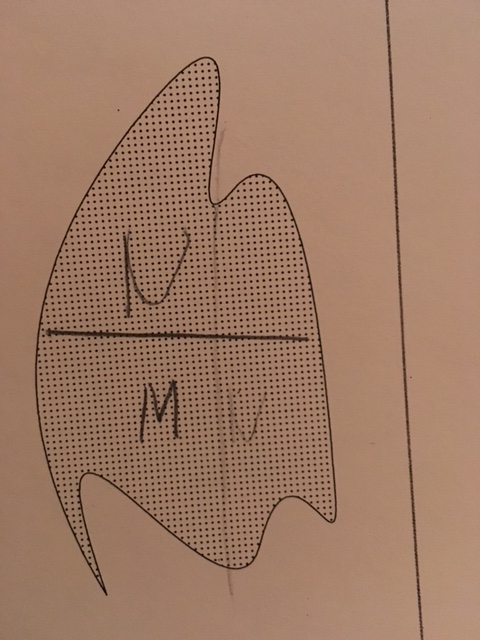
This group had had a number of fits, but with the divider-chooser, they were able to find a balance more quickly than in previous attempts.

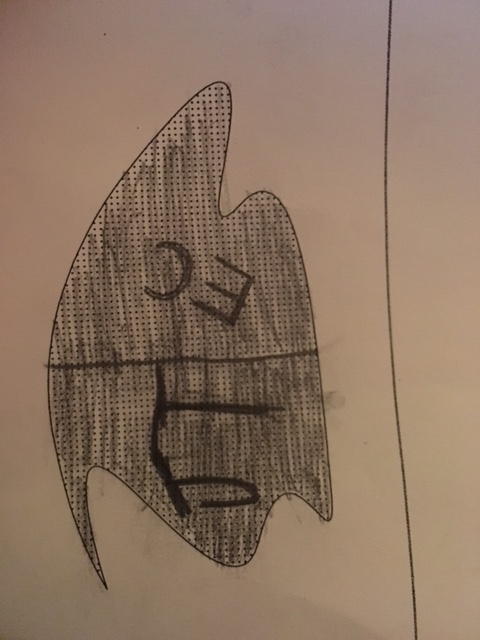
Another nice horizontal split.

One thing to note about all these divisions: most of the groups were engaged in cooperative sharing. So, a method like the divider-chooser was generally overruled by a group decision if the chooser felt that they were getting a larger share. The students knew that they were supposed to share fairly and so if the situation turned unfair, they self-corrected.

Something like the divider-chooser method is good in adversarial settings where one side is aiming to bilk the other side. To some extent we had anticipated this meta-behavior. What was encouraging though was that there were a few groups, who prior to the divider-chooser method, had clear imbalances [we helped correct them as we went around by asking questions like “if this were a cookie, would you be happy with your part?”]. However, with divider-chooser, the sharing became more fair since both sides made decisions and had incentives to create a situation that benefited them the most.

Now, there are some biases with divider-chooser, but for the purposes of second grade, this exercise was sufficient.

The next thing we wanted to do was to add a tactile aspect to this with a real incentive to create a situation of self-interest. For this, we brought out Play-Doh and the incentive that they get to play with it once they have split it in a way that everyone can agree to. The additional twist? They now have to be in groups of four.

Continue on to Part 4.