Tag Archives: probability

Correlation Does Not Imply Correlation — A Message For The Data Scientist

Leave a reply

You’ve probably heard the mantra “correlation does not imply causation” in a stats class or in some heated debate where eventually one side has to “statsplain” to the other side that just because two events have a link (correlation) the causality can’t be inferred. In fact, sometimes correlation can be spurious, especially when we compute lots of correlations and the sample size is low. One good example of this can be found on Tyler Vigen.

But I bet you’ve never heard the saying “correlation does not imply correlation”. What does that even mean? Let’s take a small mathematical jaunt, shall we?

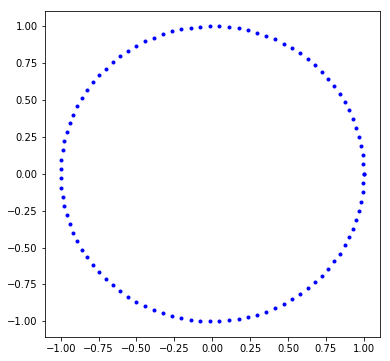
Are these set of points correlated?

Are these points correlated?

Here is the code that generated these points

r = 1
theta = numpy.linspace(0,math.pi*2,100)
x = r*numpy.cos(theta)
y = r*numpy.sin(theta)

and if I compute the correlation coefficient via

numpy.corrcoef(x,y)

I obtain this output, which effectively says that the correlation between \(x\) and \(y\) is zero!

array([[ 1.00000000e+00, -1.11038848e-17],
       [-1.11038848e-17,  1.00000000e+00]])

But clearly, these are points the points of a circle! How are they not correlated? Let’s take a look at a few more examples.

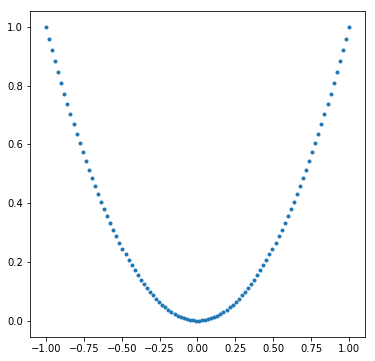
Here is \(y = x^{2}\) sampled on \([-1,1]\)

What’s the correlation coefficient between \(x\) and \(y\)?

And the correlation between the \(x\) and \(y\) values is … drum roll, please … zero!

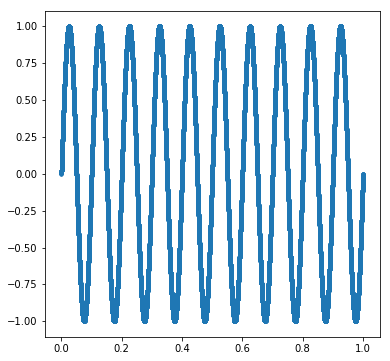
Ok, two more examples! Here is \(\sin(20\pi x)\) on \([0,1]\). Correlation coefficient is -0.078, which is not exactly zero. But it’s also not exactly 1 (perfect positive correlation) nor -1 (perfect negative correlation).

\(\sin(20\pi x)\)

And our last example, \(\sin(21\pi x)\), which produces a correlation coefficient of zero!

What’s the deal?

Is there a functional relationship between \(x\) and \(y\) in the graphs above? Yes!

So why is the correlation zero? The dirty detail is that the type of correlation that is computed is linear correlation. And there’s a great deal written about this. Wikipedia as usual gives an extensive amount of detail. You can go further down the rabbit hole and learn about “rank” correlation. The former being Pearson correlation, the latter being Spearman correlation.

But that’s not the point of this article. The point is about the dissonance between our casual, colloquial understanding and use of “correlation” and the canonical mathematical definition. Often, when we speak of correlation we really mean something fuzzy and vague like “patterned behavior”, “relationship”, “association”, etc. and we expect that when a pattern emerges in the visualization of the data, it should be corroborated by a mathematical computation of correlation.

You’ll find that when the question is phrased as “What’s the correlation between [unordered / unorderable input] and [response]?” we’re in this territory of correlation not implying correlation. The questions are either unanswerable or otherwise not actually asking for correlation. Rather the request is for a search of some, not necessarily linear, relationship or grouping of the data.

In practical settings when discussing data with a mixed technical audience, if you happen to be the data person, it is important to hear the multiple contexts of the words people use. The data analyst, data scientist, statistician, mathematician, or in general the person responsible for producing an analysis of data, has the burden to carefully parse the language spoken by their colleagues and to help reframe it into a mathematical statement. If the request cannot be put into a mathematical framework, that in and of itself is progress and should inform you that to answer the question at hand, perhaps, should be asked elsewhere.

Here’s one question I got in an interview several years ago: What’s the correlation between domain and our game’s user acquisition costs? This question doesn’t make any sense. Domain is not a number. What the person was really asking for was something along the lines of “What are some commonalities between the domain we purchase users for our game and how much we pay?”. There is no “correlation” to compute. Instead, this is more about clustering or possibly just producing a bunch of histograms. I was able to redirect the conversation to their actual wants rather than taking the question literally as a request for a computation of a correlation coefficient.

So ye be warned: Correlation does not imply correlation!

And Now From The Twitterverse!

We have some nice finds!