How much integration should we really be teaching?
Let’s start with a standard example, $$\int \frac{dx}{(x-2)(x-5)}.$$ The idea is to rewrite the integrand as $$\int \frac{-1/3}{x-2}+\frac{1/3}{x-5}\ dx.$$ A pair of simple substitutions give us $$-\frac{1}{3}\ln|x-2|+\frac{1}{3}\ln|x-5|+C.$$
Is this a useful thing for a calculus student to learn? There are some good reasons why not. First of all, the key step — partial fractions — is not calculus. It’s just algebra, although it is certainly motivated by calculus. Secondly, is expressing this integral as a weighted sum of shifted logarithms useful? And is this method something a typical student is even going to remember two weeks after the class ends?
That last question drives a lot of my course design. I loathe “tricks” because no one will remember them when it comes up again. I’d rather invest time getting a deeper understanding of analysis of functions so the student can easily synthesize whatever tricks he or she needs when it is relevant. A sort of “teach a man to fish” philosophy.
That said, I do think partial fractions are important. You are demonstrating that integration is not always just “spot the right form.” You are also giving more experience working with rational functions, and hopefully through the mechanics of finding those numerators the students are learning something about why these expressions can be manipulated in this way.
But then we get to $$\int \frac{2x^2-x-1}{(x^2+1)(x-2)}\ dx.$$ The decomposition of this one is $$\int \frac{x}{x^2+1}+\frac{1}{x^2+1}+\frac{1}{x-2}\ dx.$$ Messier, but doable. The algebra requires more thought about what those denominators should be and it is a larger system of constants to find. Have we bought anything pedagogically from this experience?
I’d say not really. The conceptual point was made in the first example, so this is mostly about execution. But perhaps the deciding point is this: if this integral came up in my own work I probably would let Mathematica do it, whereas I’d do the first one by hand. So not only is it mostly about execution, it’s about execution of a skill that technology has devalued.
It’s not just about technology. The bias toward getting integrals expressed in terms of elementary functions is damaging to students’ abilities to work with functions in general. There is a lot of emphasis on being able to plug values into a function when that is rarely what you ever actually want to do.
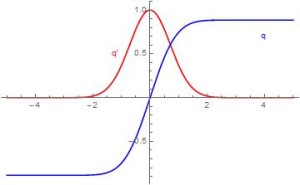
For example, consider $$q(x)=\int_0^x e^{-t^2}\ dt.$$ This function is not on my calculator (actually something much like it may be, but we’ll get to that). I can calculate q(0)=0 pretty easily, but even though I have no hope of getting any other values by hand, I can quickly tell you that it has no other zeroes, it is always increasing, it is concave down exactly when x>0, and the function is odd. I can do that because the Fundamental Theorem of Calculus tells me $$q'(x) = e^{-x^2},$$ which is always positive (so q is increasing) and q’ is decreasing for x>0 (so q is concave down). The fact that q is always increasing tells me that once I find my zero at q(0)=0, there won’t be any more. I also recognize that q(x) has horizontal asymptotes because $$e^{-x^2} < e^{-|x|}$$ for large x, and also q(x) must be odd because q'(x) is even and q(0)=0.
And when the student complains that this is just some contrived function that only a cruel professor would care about, you mention that after I throw in a few constants, this is the cumulative normal distribution function. It is important in statistics. I don’t mean “sometimes it comes up” important, but “used every day, you do not understand statistics if you do not understand this function” important.
So where do we draw the line? First observe that there are really only two elementary integration techniques, substitution and integration by parts.
Substitution always starts with something like $$\int \sin 6x\ dx,$$ which is nice because you can get it right by guess-and-check before learning the rule, which is really just a generalization of what you were guessing and checking: reversing the chain rule. Similarly, integration by parts reverses the product rule.
There aren’t really any more differentiation rules to reverse. The sum and constant rules are used all of the time, but they are usually established well before this point in the course. The quotient rule does not reverse nicely and is really just a combination of the chain and product rules anyway, since $$f(x)/g(x) = f(x)(g(x)^{-1}).$$
All of the other integration techniques we learn are just clever applications of these rules. I can calculate $$\int \frac{dx}{\sqrt{9-4x^2}}$$ with a substitution, but one needs to learn to recognize how trigonometric identities help here. Similarly, I can calculate $$\int \sin 6x \sin 7x\ dx$$ using some different trigonometric identities. I cover the first type of problem in my course but not the second, but I’m not sure I can give you a good reason why beyond “it’s what the text does.” (And in case you are wondering, we use Hughes-Hallett, et al, which I actually quite like and from which I lazily stole many of my integration examples above.)
One integration example I always do is $$\int \sec x\ dx.$$ The trick — and it is a trick — is to multiply by $$\frac{\sec x + \tan x}{\sec x+ \tan x}$$ and use the substitution w =sec x+tan x. For no particular reason, everything works out and you somehow get ln|sec x+tan x|+C. I show this to illustrate that sometimes mathematics is about pulling a rabbit out of a hat, but I do not expect anyone to regurgitate this ungeneralizable shenanigan.
I cover fewer tricks now, having swapped out that time to give students a bit of experience with computer algebra systems. I wish we could cover everything, but there just isn’t time and we must make thoughtful decisions about what best serves our students. I personally value depth over breadth and this isn’t the first time I’ve written about expendable content in calculus.
Ultimately it is a matter of taste. I am wary of teachers being micromanaged on coverage, because what works swimmingly for one teacher may not work for someone with a different style and point of view. And that needs to be OK.
Bill Wood @MathProfBill is an assistant professor of mathematics at the University of Northern Iowa.