This post is part of the ppmmc series. Please make sure to have read the previous posts in the ppmmc series so that the context is understood.

A Very Introductory Introduction to Markov Chains

In this post, we will introduce Markov chains. We will mix in some programming as well. Again, as was the same case with Monte Carlo methods, we are going to try to keep this intuitive and go a bit light on the math. Conceptually, Markov chains can be understood without having a heavy background in mathematics.

We will use equations from time to time, but will supplement them with words. Thus, if you are not versed in probability theory, don’t worry, just read along. For the reader who wants to go further on her own, here are some search terms that she can use along with
“Markov chains”:

• transition probabilities
• transition matrix
• absorbing state
• ergodic (or irreducible)

A Simple Game

Let’s consider the following dice game. Consider a six-sided die with the faces numbered
\(\{1,2,3,4,5,6\}\).
The rules of the game are as follows:

1. Roll die.
2. If the number is odd, then go to L.
3. If the number is even, but not equal to six, go to Step 1.
4. If the number is equal to six, then go to W.
12. Sorry! You lost!
23. Great job! You beat the odds and won!

Now, how would this look if we were to draw this out in a
“state diagram”?

It ought to look like this:

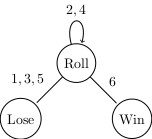
With this simple game, we can start to classify a few things. The “Lose” and “Win” states end the game. These are called absorbing states. The states that don’t end the game are called transient states.

Next, we can ask these questions:

• What is the average number of rolls it takes for the game to end?
• If we win, what is the average number of rolls it takes to win?
• If we lose, what is the average number of rolls it takes to lose?
• What proportion of times do we win?

We can answer these questions exactly with a little bit of math, of course. But what if we couldn’t? What if we were stuck? We can always write a program and get good estimates via simulation! So let’s do this.

First, we have to know what we’re going to do. Here we list out a few items:

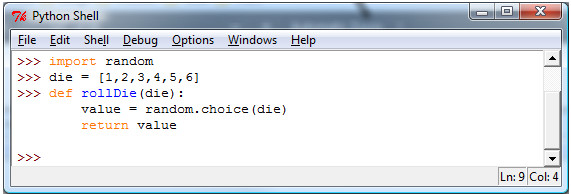
• We have to write a method to roll the die.
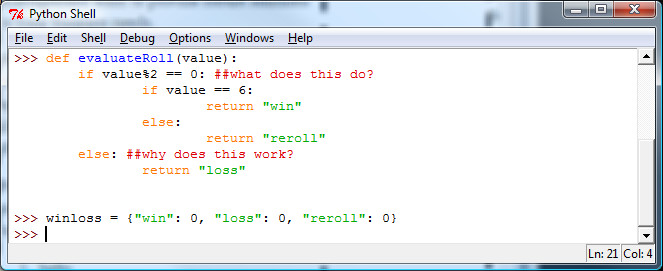
• We have to evaluate if we won, lost, or get to roll again.
• We have to keep track of our wins and losses.

Instructors: As you may be able to tell we’re building up to working with classes. This exercise won’t yet use classes.

Here is our rollDie method.

Next, we have to evaluate the die roll and we need a variable to keep track of wins and losses. There are many options, but for fun, we’ll use a dictionary.

Now, we can finally run simulations.

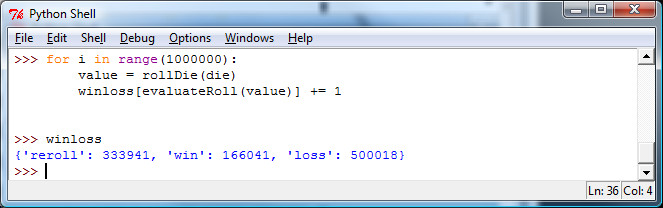
So, according to this, when we rolled the die one million times, 333,941 times we had to reroll, 166,041 times we won, and 500,018 times we lost. Does this make sense?

Let’s think about this. According to the state diagram that we drew, two out of six times we would have to reroll. One out of six times we win and three out of six times we lose. This looks to be inline with what the simulation says.

Ok, so we have covered quite a bit right now. In the next session, we will get a bit more sophisticated. In the next session, we will evaluate what happens when we play one million
games rather than one million rolls.

Don’t hesitate to get in touch if you have questions or would like more information about setting up a workshop or training in your school.