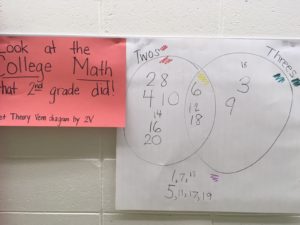I went to second grade again this year for my annual math visit. This marks my fourth visit in total and this year we explored Set Theory. In previous years, we explored Graph Theory and Self-Organizing Systems, Cryptography, and Fair Sharing. I’ve taught Set Theory units previously to my college students and I wanted to bring at least the first college lecture to second graders.
Here’s a glimpse of what some of it looked like and the rest of this article gives the play by play!
#BedminsterSchool Mrs Valentine & Manan’s annual #collegemath lesson in #Gr2 today! #SetTheory Ss became members of a set & learned about elements of sets: unions, intersection, #VennDiagram . So happy to see Ss in action thx! @settheory @gcouros @settheorytalks pic.twitter.com/lEVdRS9Ki6
— J Giordano (@jgiordanobts) June 14, 2018
Now, the second grade teacher is my wonderful wife, Mrs. Valentine (Meredith). 😀 We had been planning this lesson on and off for the past few months. It was important that we taught this lesson as closely to the same way I would teach to a freshman college class.
The first thing I do with a new classroom is to learn the students’ names, college or in second grade. To that end, I arrived about 15 minutes before class started and committed to memory everyone’s name correlated with their designated seat. As the school day began and the students settled into their morning routine, I noticed that this class was unlike previous classes I had visited. Normally, I would hear not-so-whispery whispers of “who’s that?” “is that a lawyer?” “is that a new teacher?” “is that a principal?”. This time, not a peep. My presence was barely noticed. Every class is different!
Anyway, morning routine — some writing work, then morning announcements from the PA and the Pledge, and finally, their morning meeting. I love their morning meeting. They sit in a circle on the rug and greet each other, handshakes, funny noises, etc. There’s also a question that the “Lucky Duck” gets to ask and students provide answers defending their reasoning. This time it was about how many days will have passed from May 25th to June 13th. All of this is a great way to build community in the classroom, especially since it’s a daily activity.
When they got back to their seats, Meredith began the introduction. Immediately students guessed who I was. Curious! They weren’t speculating openly earlier when they walked in because they already knew who I was. Before we started our lesson we spent a few minutes getting to know each other.
“Raise your hand if you play a musical instrument.” “Raise your hand if you play the piano.” “Raise your hand if you like to play games.” Look at all the things we have in common!
Next, let’s make introductions. I had students cover up their names on their desks. And now my task was to make sure I could name them all. And lucky for me, I got everyone’s name correct. Ok! Now we’re ready to begin.
Math In Motion
If you have ever taught, you know how important it is to get students to move. College classes tend to be a lot of sitting, but even there I try to get some motion. So our first exercise went like this.
We had all students stand. In the back there were stacks of colored paper. Our first task: “Everyone who is wearing shorts, grab a yellow sheet of paper.” Next, “Everyone who has long hair, grab a blue sheet of paper.” (They could decide if they had long hair.) And finally, “If you didn’t get a piece of paper, grab a purple sheet of paper.”
Now, if you are familiar with what an introductory set theory lecture may look like, then you know we are going to want to introduce Venn diagrams and the ideas of intersection and union.
Our first question was “What does it mean if you are holding a yellow sheet of paper?”. Of course, this was an easy question for our brilliant second graders. It meant that you were wearing shorts! “What does it mean if you have two different colors of paper?” This is an important question and we weren’t sure how students would respond. But our first student to respond said, “It means that you are wearing shorts AND have long hair.” What a perfect answer! He got a high five and we paused for one second. I wanted to repeat the sentence and put extra emphasis on our immensely important vocabulary word: AND. It may seem trivial, but AND is very important in our introduction to Set Theory.
I wrote AND on the ActivBoard and told our students to remember this important word. Next we discussed the blue sheet of paper. And finally, we moved to the purple sheet of paper. What did that mean? Again, a brilliant response: “It means that you’re not wearing shorts AND you don’t have long hair.”
Discussing sets using students as elements of sets can be a little tricky and we have to be mindful that, especially with younger students, we don’t create a sense of exclusion. But sets by their very nature, include elements and exclude elements. This is why we made sure that every student got a piece of paper. And so, we re-iterated that everyone who is holding a piece of paper (which was everyone) had something special about them. That is some people have short hair. Some people are wearing long pants. Some students had both short hair and were wearing long pants.
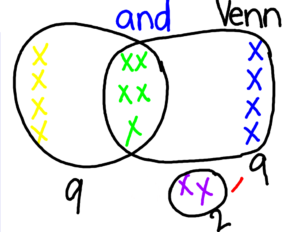
Now, we paused for a second since we needed to do a little drawing and a little counting. The image below is what we came up with. [What color do we get if we mix blue and yellow? Green!]
And our counting? How many students have long hair? Nine. How many students are wearing shorts? How many students are holding purple paper? Two. How many students are there in total? Fifteen! But what’s \(9 + 9 + 2\)? Twenty!
Aha! So why did we add to 20 but there are only 15 students? Never underestimate second graders! One girl answered [not an exact quote], “Well, we counted the people with blue and yellow papers twice. And if you take away five we get fifteen.” Yes!! Inclusion-Exclusion!
One thing I want to emphasize: The abstract representation of each student to a colored “X” was directly understood. And the grouping into “sets” also was well understood. We discussed what the green “x”s meant and why they were “in” both circles. Again, we received great responses to the meaning of the abstract representation as it was reinforced (and introduced first as) via the physical, tactile exercise of constructing a Venn diagram [they were the elements!].
Now it was time for them to make their own Venn diagram.
Using the alphabet!
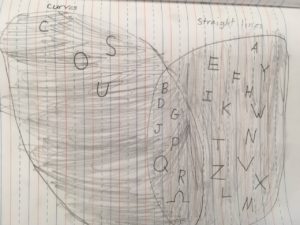
When introducing new concepts, I do everything I can to avoid using new contexts. The alphabet is well understood for second graders. This was an individual or a group exercise and it was their choice (actually one student requested if they could work in groups!). Their task? Make a Venn diagram that separates the letters into those with “curves” and those with “straight lines” [we made sure to define / clarify this if there were questions]. Here is one sample of a student’s work.
If you are wondering about the \(\Omega\) we later introduced the idea of a “universe” and gave it the label of \(\Omega\).
We had a great discussion about the alphabet here. Some students argued that the “S” should be in both curved and straight lines. One student said that all letters would be straight lines only if they were written the way a microwave would write it! We talked about “G” and “U” as well. Every student had their own Venn diagram.
Intersection
Not shown in the above, is our introduction of the vocabulary word “intersection”. We revisited our “shorts and long hair” grouping as well as looking at our alphabet and talked about the “things in the middle”. Up until now, when asked where, say, “R”, should belong, students would say “in the middle”. So, after they had all finished their Venn diagrams, we decided to do the exercise again as a class. We had already done A, B, and C. Our next letter was “D” and at this point, I introduced the word “intersection”.
We had a great conversation about where else we might have heard the word “intersection”. One student said that they heard it when adults were talking about going to a meeting (interesting!). One student talked about when two roads meet. We related these concepts to our sets (and to note, we used the word “set” regularly without explanation — they picked up on the usage). What does the “intersection of curved line and straight line letters” mean? Students: “it means that some letters have both straight and curved lines!”. The use of the word “both” was critical and we tied it back to the use of “and”.
From here, as we finished up the alphabet, every time a letter was “in the middle”, we made sure to say that the letter was “in the intersection” of the two sets. Focused repetition to reinforce a new term without contextual overload. Now they’ll always have at least one mental model to fall back on when thinking about the intersection of two sets.
Would you know that at this point, we were one hour into this? And there was no stopping them.
They had a lot more energy and engagement left in them. So, we decided to introduce some formal notation.
Notation!
Believe it or not, this part was the easiest of the lesson to convey. Second graders can process and accept abstract notation far more easily than we may be predisposed to believe. Here’s all I did, I asked about \(1 + 1 = 2\) and we talked about the “symbols” of \(+\) and \(=\) (using their own words). Then, I introduced our symbol for “intersection”. Here is our ActivBoard.
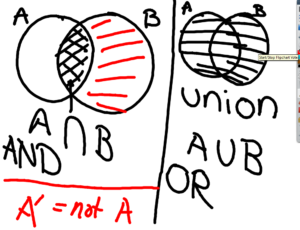
Next, we talked about “AND” and “OR” and introduced some more notation. We learned to read this as a full sentence, as well!
What an amazing moment — new symbols, new concepts, no problems! At this point, I made sure to remind them that what they are learning right now is no different from what I would teach in college. And that if today, here in second grade they could do college math, then in third grade they can do third grade math, in fourth grade they can do fourth grade math, and that they can always do math! More than a few students’ faces lit up.
Ah, but math! What kind of math do we do in second grade? One student said, “We do addition, subtraction, multiplication, measuring, time, and stuff like that.” Did I hear multiplication??
Common Multiples and Sets!
Second graders, by this time of year typically get some introduction to multiplication. One first introduction is via “skip counting”. Skip counting by twos (without any offset) means “2, 4, 6, 8, …”. Skip counting by threes means “3, 6, 9, 12, …”. How does this relate to sets?
We need to start moving again. Have a watch of this video I made some time ago about discussing common multiples with movement. We are literally “skip counting”! The long and short is that we had two students walk together step for step. However, one student only says the numbers encountered when skip counting by twos and the other when skip counting by threes. What happens? Of course, at 6, 12, 18, … both students speak at the same time!
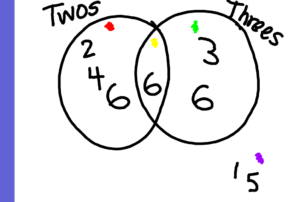
Now, we moved to Venn diagrams! We had each student come up the ActivBoard and write their number (sequentially) into the appropriate set. Does the number reside in the “twos”, the “threes”, the intersection, or none of these? With 1, 2, 3, 4, 5 we made some great progress. Then we got to six. Here was our first attempt to decide where to put 6.
First, the six should have been in the “twos” only group. But then we realized it should be in the “threes” only group. But then we realized that it should be in the intersection! Aha!
Of course, there was a technical glitch with the ActivBoard, so we moved over to our paper and pencil easel. Here is what our final Venn diagram looked like when we counted up to 20. (Eventually, this was hung up in the hallway outside of the classroom as the students were super proud of their accomplishment!)
A final challenge
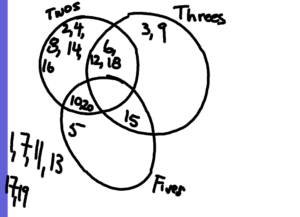
Well, now, almost two hours later, it was time to be done. As they left for lunch, I left them a challenge problem on the ActivBoard using three “circles”. If we skip count by twos, threes, and fives what would our Venn diagram look like?
Here’s what I put up for them to tackle.
When they came back to the classroom from lunch and were getting ready for recess, we showed them the challenge problem. They began interpreting this new Venn diagram and what the numbers meant. We asked them what would be the first number that would go into the empty region. They headed off to recess with this problem in mind. No doubt forgetting about the problem. When they came back from recess, I had left, but Meredith tells me this:
“Several students took up the challenge and one student reasoned that the first number in the intersection of all three sets should be 30 because if we count by tens we would get 10, 20, 30. But if we count by fifteens, we would get 15, 30 and so the first number should be 30.” Not bad!
And that was my visit to second grade this year. If you’re interested in more, you can read about some of my previous visits (Graph Theory and Fair Sharing). And if you’d like to do this for your classroom, get in touch and let’s see if we can work out an arrangement!