What Are Primal Words?

Leave a reply

You probably know me as the guy who invented “semi r-primes” and “emir prime” as well as “funny numbers”. In this article, we’ll talk about primal words. What are they? How do we construct them? And are there any statements we can make about their existence for an arbitrary word?

First, let’s see if you can guess what’s happening here. I asked this question on Twitter:

SPOILER ALERT!

Read no further if you are still guessing. Otherwise, continue.

Both @jonathanavt and @noswald figured it out!

Their responses

Now, given the two examples I gave these responses are clearly correct. Here are some other examples.

word prime mapping
MATH 1120071599 M = 12, A = 00, T = 71, H = 59
MISERY 11208180417503 M = 12, I = 08, S = 18, E = 04, R = 17, Y = 50

We should notice that for MATH, we have that T = 71 rather than 19. Similarly, H = 59 rather than 07. The full mapping of letters to two-digit base ten codes follows this progression.

a b c d e f g h i j k l m n o p q r s t u v w x y z
00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51
52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77

So what this means, and by example, is that A can take on 00, 26, or 52.

Now we are in a position to discuss primal words.

What is a primal word?

We’ll define a primal word in a broad capacity — a primal word is a sequence of letters (“word”) that can be uniquely mapped to a prime number under the following construction. First, we need a collection of letters — the American English alphabet with its usual A-Z ordering. Next, we will construct a multi-value map / encoding from letters to a triplet of two-digit encodings. \(A \rightarrow [00,26,52], B \rightarrow [01, 27, 53], \ldots, Z \rightarrow [25,51,77]\). Notice that the two-digit encodings ranging from 78-99 are excluded.

The construction of a primal word, then, proceeds as follows. Let \(W\) be a word consisting of a specific arrangement of \(N\) letters, \(L_{N}L_{N-1}\ldots L_{1}\). Since each letter \(L_{k}\) can be mapped to one of three 2-digit encoding possibilities, we have \(3^{N}\) possible encodings of length \(2N\). Let \(X = [1,2,3,4,5,6,7,8,9]\) and \(Y = [1,3,7,9]\). Let \(f_{i_{k}}, i \in \{1, 2, 3\}\) be a choice function that selects the \(i\)th encoding for the \(k\)th letter in \(W\). Thus, for the word “MATH”, \(f_{1_{3}}(“A”) = 00, f_{2_{3}}(“A”) = 26\), etc. Then, the concatenation of \(x \in X\) with one of the \(3^{N}\) encoding possibilities and \(y \in Y\), where \(x\) is to the left of the encoding of \(L_{N}\) and \(y\) is to the right of the encoding of \(L_{1}\) yields \(9\times 3^{N}\times 4\) possible \(2N + 2\)-digit numbers. The smallest of these numbers that is a prime is the unique prime number that maps to the word, \(W\), if a prime number exists. If such a prime number exists then \(W\) is a primal word.

That’s a mouthful. Let’s see some more examples!

Examples

words first_prime
inaugurations 1081300200620170019081465183
elderlinesses 1041103041711081304181830189
preformulate 11517040514171220110045563
dowry 103142243249
doeskins 103140418100813189

But what if I did something like “AAAAAAAAAA”? Well, it turns out that 1000000000000000026263 is a prime number and is the first prime number using the encoding possibilities for A and prepending from the choices available in \(X\) and appending from the choices in \(Y\). Thus, “AAAAAAAAAA” is a primal word.

Conjectures

The real challenge for you is can you find a word that is not primal? So far, I’ve been unable to do so. In fact, consider the previous two sentences. Converting them into prime encodings (ignoring characters that are not the letters A through Z), we have

11907047 1170400111 10207001111043932563 10514171 12414469 108187 10200139 12414469 1050813037 1009 1221417551 1190700191 108187 11314717 11517081200377? 118147 10500431, 108’21043 1010404133 12013000137301 145661 103141 118147.

You’ll notice that each of these primes had a leading digit of 1. Every example I’ve tried only ever needs a leading digit of 1. So, I have two conjectures.

Conjecture 1

Every word is a primal word.

Conjecture 2

All primal words have a leading digit of 1.

Sketching Proofs for Conjectures

A word of length \(N\) maps to an encoding of \(2N + 2\) digits. For a word of length \(N\), there are \(36 \times 3^{N}\) encodings to consider. A number that is \(2N + 2\) digits long is in the range of \([10^{2N + 1}, 10^{2N + 2})\). Now, we know that an approximation to the number of primes less than \(x\) is \(\frac{x}{\log(x) – 1}\) where \(\log\) is the logarithm with base \(e\), the natural logarithm. So, in the range just mentioned, there are approximately $$q_{N} = \frac{10^{2N+2}}{(2N+2)\log(10) -1} – \frac{10^{2N+1}}{(2N+1)\log(10) -1} \mbox{ primes}.$$

Now, it doesn’t take too many guesses to land on a prime. In fact, if there are approximately \(q_{N}\) primes out of \(r_{N} = 9\cdot 10^{2N+1}\) numbers in \([10^{2N + 1}, 10^{2N + 2})\), then we would need on average \(g_{N} = \frac{r_{N}}{q_{N}}\) guesses (with replacement) before we land on a prime (eg, generating a 20-digit prime (word of length 9) requires 45 guesses on average). However, we have at our disposal \(c_{N} = 36 \times 3^{N}\) guesses (eg, for a word of length 9 we have over 700,000 encoding possibilities vs the average 45 guesses needed to land on a prime). As \(N \rightarrow \infty\), \(\frac{c_N}{g_N} \rightarrow \infty\) and in fact, for every range of power of 10, \(c_{N} \mbox{ is so much greater than } g_{N}\) that it is statistically unlikely that a prime number could not be found for any given word of any given length.

As for conjecture 2, fixing the leading digit to 1 means that we have \(4 \times 3^{N}\) guesses rather than \(36 \times 3^{N}\). This factor of 9 reduction is not enough to change any of the statistical conclusions.

So now that you’ve learned what a primal word is, let’s classify them a bit more. Let’s talk about “primal words of order \(k\)”.

Primal Words of Order \(k\)

Suppose we have a 2-letter word. We would search for its primal-word-making prime number by starting at the smallest admissible 4-digit encoding for that word and proceed in an ordered progression until we encountered a prime number. So, we define a “primal word of order \(k\)” as one less than the number of encodings we had to search through. For example, the word “AB” is a primal word of order 3. Why? First, \(AB \rightarrow 100019\). To arrive at 100019, we had to first check 100011, then 100013, then 100017, and finally 100019. The first three encodings were not prime, the fourth one was. Thus, “AB” is a primal word of order 3.

Having this naming system allows us to write down prime numbers by simply remember the word and its order. For example, if I tell you that the word “PRIME” is a primal word of order 2, you can write down the prime number immediately. In fact, it is 115170812047 because the first two attempts, 115170812041 and 115170812043 are not prime.

See if you agree with the order of these words.

words first_prime order
decoupage 10304021420150006047 2
icebreaker 1080204011704001004173 1
crewnecks 10217042213040210181 0
counterpicketed 10214201319041715080210041904033 1
degum 103040620121 0

The word with the largest order that I’ve been able to find is QUINTUPLICATING with an order of 375! I haven’t tried made up words yet. It is an open challenge to the reader to find a word with higher order.

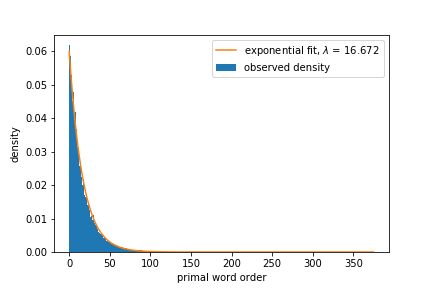
Here’s a density plot of primal word order on the ENABLE word list.

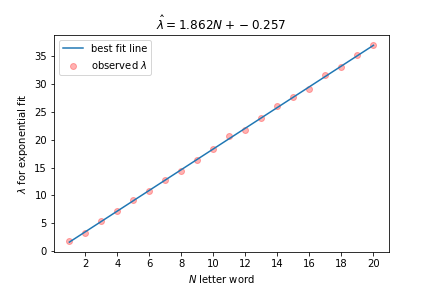
Density Plot of Order of Primal Words from ENABLE

Notice the very nice exponential fit with \(\lambda \approx 16.672\). If I generate \(N\) letter words for \(N = 1, 2, \ldots, 20\) and apply exponential fits for each \(N\), then the \(\lambda\)s grow linearly with \(N\). Here’s a plot of how \(\lambda\) changes as the word length increases. The regression line explaining \(\lambda\) is \(\hat{\lambda} = 1.862N – 0.257\).

Linear regression on exponential fit parameter, \(\lambda\), as word length, \(N\), increases

You may have noticed that on the entire ENABLE data set, the $\lambda$ parameter was approximately 16.672. This implies an \(N\) of about 9.09. The mean length of a word in ENABLE is 9.09, which is a nice corroboration of results.

And this my friends, is math recreation. 😀

If you’re interested in an interactive version, just sign up or leave a comment below, if you have already signed up. If I get at least 5 requests, I’ll make an interactive one!

In other world news

I posted this little “contest”. Check out the thread to see the awesome submissions by @AeroDaveLowe, @aap03102, @math_doc_ron, @acoustionicus, and @CardColm.

Leave a Reply

Your email address will not be published. Required fields are marked *