It’s that time of year again! Up here in the northeast US, the autumn air is coming. The sun starts setting noticeably earlier. The birds start to take flight. You apparently can’t wear white after Labor Day. And good luck getting one full week of school until mid January. It’s back to school time!
So, what did you do this summer? Did you go down any slides? How about a summer slide? You know that thing that happens to kids if they are playing in the summer and not focusing on academics. :eyeroll:
Anyway.
Yes, there’s likely some loss of knowledge. But it can be brought back fairly quickly.
This post is for those going into second grade [parents, teachers, and students]. Here are five quick warmup exercises to get your kids loving math, moving to math, and remembering math. Teachers know this, but if you’re a non-teacher, it may not be obvious: new second graders are still first graders!
Warmups!
Activity #1 Hop to it!
Have students partner up: student A and student B. Start with basic counting. Student A hops in place and yells, “one!”. Student B, next, does the same but yells, “two!”. Students alternate until they get to 10 or 20 or whatever your (or their) choosing. Got the heart rate up a little? Now do the same routine, but have them skip count by 2s or 3s! So, it goes student A: hop, “2!”; student B: hop, “4!”, student A: hop, “6!”, etc.
Activity #2 Greetings!
Put students first in groups of 2, then 3, then 4, then 5. Have them introduce each other by shaking hands with each other. Have them count the total number of unique handshakes in their group. In a group of 2, there is 1 unique handshake. In a group of 3, there are 3 unique handshakes. In a group of 4, there are 6 unique handshakes. In a group of 5, there are 10 unique handshakes. Record this data on your whiteboard so that all students can see. Ask them, “How many handshakes in a group of 6?” Let them try to work it out. There are many ways to do this: graphically, computationally, and physically acting it out. There are 15 handshakes in a group of 6.
This is a great way to break the ice!
Activity #3 How many superhero costumes?
Our second grade superhero wears a mask, a cape, a shirt, and pants. The mask is either blue or red. The cape is black or red. The shirt is green or blue. And the pants are red, green, or black. How many different outfits can we make?
Use crayons! Use paper! Can they find all 24 outfits?
How is this math? It’s secretly multiplication and the fundamental theorem of counting!
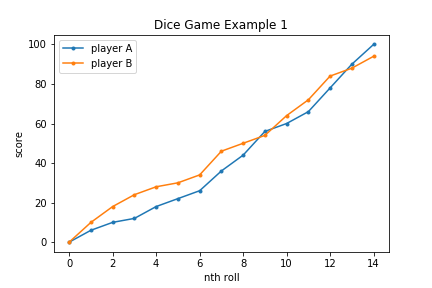
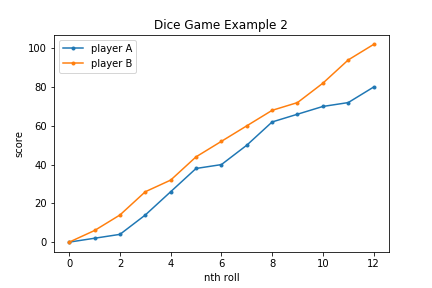
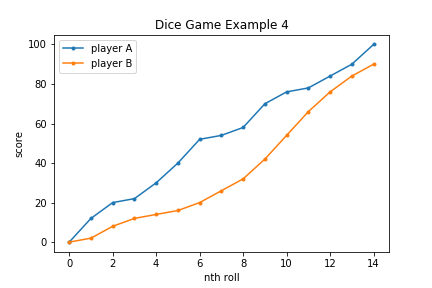
Activity #4 Race to 100! With a twist!
You can do this activity in groups of two or more. I’ll show you how with a group of two. One student (A) has one, standard, six-sided die. The other student (B) has two, standard, six-sided dies. Each student rolls their respective die / dice. Since student A has one die, she doubles her roll. Student B rolls both and adds the total number of pips. Each student starts with a total score of 0. Each round they take the value of their and adds it to their total. Who gets to 100 first?
We’re practicing doubling, adding, and adding “big” numbers. This one can be a little difficult on their first day back, so save it towards the second week. Some students may not feel comfortable adding 28 + 11 for example. They can use whatever strategy they want (directly counting, tally marks, etc.). You can also shorten the game to end at 25 or 30 if you want students to ease into this.
Here are a few sample games
Activity #5 Let’s TALK math!
We don’t just have to practice our mechanics. A fun and simple activity that I think is not used nearly enough is to go around the classroom and have students say math terms. It’s that simple. Start with someone and go around the classroom. Each student says a math term they know. And they keep going until they run out of math words. Some caveats: you probably want to set up a rule that says that they can’t just start saying numbers or numerals. In other words, you can disallow “one”, “first”, “million”, “billion”, “point zero one”, etc. Instead, you are looking for students to say things like “math”, “add”, “addition”, “multiply”, “multiplication”, “fraction”.
What’s useful about this? It’s an absolute essential for the teacher to understand what students have heard. It gets students to hear words that maybe they haven’t heard before — crowdsourcing vocabulary! You can also crank it up a level if they can define or otherwise explain the term. You’ll be surprised to hear what they say!
Try these exercises! Let me know how it goes! And I kid you not, the most important one is activity #5. Don’t underestimate this!
And now from the Twitterverse
Puzzles and more the Twitterverse
Long overdue but check out this thread with all the gems. Winners are @daveinstpaul and @icecolbeveridge
next blog shoutout challenge!
real <—> ideal
complex <—> simplexthese are two examples of a pair of #math words whose Levenshtein distance is 2. Can you find a pair of math words that have Levenshtein distance 1?
see next tweet for constraints and additional details
1/2
— M Shah (@shahlock) July 22, 2019
I've gotten a lot of great submissions! Any others?
Hoping someone will find one involving an x. 😀 I have one in mind. https://t.co/SOmqwsEnSG
— M Shah (@shahlock) July 23, 2019
Next, we have a puzzle from hella ago and I clearly gave it longer than a week.
so far only two folks have solved this!https://t.co/DHfnN7WKeP
I'll give it another week before I post solutions. Let me know if you think you've got it!#mtbos #mathsed #mathrecreation
— M Shah (@shahlock) July 4, 2019
The solution?
It’s keyboard distance assuming a QWERTY set up! How does keyboard distance work? Well, there’s no standard. But given the clues I gave, I was looking for a “keyboard coordinate system” and then apply Manhattan distance.
The keyboard coordinate system works like this. Pick a reference point, say Z. It has coordinate (0,0). Then A has coordinate (0,1), and Q would have (0,2). Then W would be located at (1,2), D at (3,1). You can think of (x,y) as “the letter at index x in row index y”. So, (5,2) the letter at index 5 in row index 2. Row index 2 is the row that Q is in. Letter index five is Y. So, the letter at (5,2) is Y.
Now, for our distance measure. I wanted to keep it “simple”, so I went with Manhattan distance. For example, “ADD” has total keyboard distance of 2 because A to D is two keys away (1,0) to (3,0) and then D to D is 0 keys away (same letter). So the total distance is 2. As another example, “MINUS” is 16. Why? M is at (6,0), I is at (7,2), N is at (5,0), U is at (6,2), and S is at (1,1). The distance from M to I is 3 (7-6 + 2-0), I to N is 4, N to U is 3, and U to S is 6, giving a total distance of \(3 + 4 + 3 + 6 = 16\).
Both @sxpmaths and @ITR13 got it.
Be on the lookout for the next puzzle and blog shoutout challenge on Twitter!