Today’s Friday Fun post is going to involve the Markov Pinball game discussed this week.

Recall the rules

1. Let’s say that the game always begins on state 1.
2. Every time we land on 4, we lose three points.
3. Every time we land on 2, 3, or 5, we gain a point.
4. The game ends once we land back on 1.
5. The transition probabilities are all equal to \(\frac{1}{2}\) and the transitions are dictated by the state diagram below.

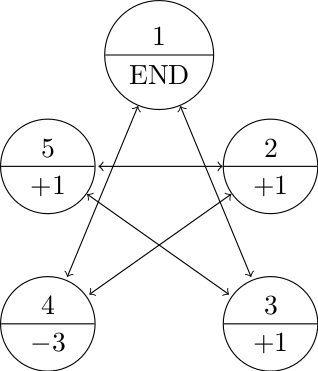
So far, we are getting somewhat convincing results (based on our theoretical and empirical calculations) that this game is fair.

However, there are a lot of things that we haven’t discussed about this game. For example, what is the probability of ending a game with a total of zero points? What is the probability of ending a game with a total of \(n\) points? What is the probability that the game will end in two steps? three steps? four steps? \(n\) steps?

Answers to these questions in full generality are not straightforward. However! As simple fun, enumeration exercises, can we count the following:

• How many ways are there for a game to end in two steps? three steps? four steps? five steps? six steps? etc. What kind of symmetries do we find?
• If we are on state \(i\), what is the fewest number of steps that we have to take to end the game? Given that we are on state \(i\) what is the probability that the game will end in the fewest number of steps possible?
• Can you find more than one way for a game to end with a score of zero?

Don’t be limited by just these questions! But let these questions spark other questions! Enjoy!