Ok! The Carnival of Mathematics #136 is here! What’s so cool about 136? First 1,3, and 6 are the first three triangular numbers. But even more amazing is that 136 is a triangular number as well! So, 136 is a triangular number whose digits are triangular! Does that make it a meta-triangular number? A fractal-triangular number? And it gets even better. The digit sum of 136 is triangular(!) — \(1 + 3 + 6 = 10\). More hidden triangularness: 1 and 36 are triangular numbers.
With all this excitement noted by !, we have to ask is \(136!\) triangular? Who wants to attempt this? We have a simple test: a number \(n\) is triangular iff \(8n + 1\) is a perfect square. Now, 136! is a 233 digit number overflowing the boundary of this blog post: $$36590428819525486576897272205198933454286172951815726156123815101405189582089242773975735166401987907830880230417721361838572072126683305250473185240276110436058808776620558462614334914409164842205184000000000000000000000000000000000$$
So, who wants to figure out if \(8(136!) + 1\) is a perfect square without tossing it into Wolfram Alpha or SAGE or any other engine? Well we can try this for calculating square roots by hand. And so begins the 136th Carnival of Mathematics.
Making Names in Life
If you know about the Game of Life by John Conway, then Making Names in Life by Matthew Scroggs (@mscroggs) shows you the initial pattern needed to spell out your name (or any name). As I played around with this a bit, I thought that this would be a cool way to create your own fictional written language. It gives a uniquely exotic or even alien feel.
Evolution
Keeping inline with the evolution theme, we have from Wim Hordijk (@WanderingWim) in his own words on Evolution: It’s as real as gravity!:
This article is about how maths plays an important role in the study of evolution. Evolution is still too often downplayed as “just a theory” (as in: a hypothesis), but in this article I show that it is just as much a valid and well established scientific theory as that of gravitation. What Darwin did for biology is on par with what Newton did for physics. I also explain some of the basic ideas behind the mathematics of phylogenetics, one of the main tools to study the evolutionary history of different species. This article just appeared in Plus magazine, an online popular science magazine devoted to mathematics.
The perfect day
49 Ways to celebrate the most perfect day of the year (This is about 6/28 … what’s so perfect about 6 and 28?) … and to piggyback off of this, Bill Wood (@mathprofbill) wrote this about \(\tau\) Day.

The Cubic Formula …
You can continue to laugh with Gregory Taylor (@mathtans) in this parody math video about the Cubic Formula.
Also make sure to check out his comic! Separation Anxiety 
Multidimensional Sphere Packing
A major breakthrough on multidimensional sphere packing — a very well written article by Evelyn Lamb (@evelynjlamb). Bill Wood is a researcher on packing methods. I’ll see if he’d be willing to write more about this.
Apollonian Gaskets
Continuing in the world of packings, Brent Yorgey (Twitter?) talks about the basics of kissing sets in two dimensions and Apollonian gaskets. In this particular case, let a picture speak a few thousand words from one of Brent’s posts
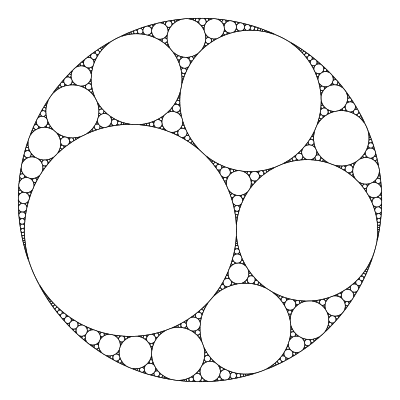
Here is the first article on Apollonian Gaskets. Then Brent gives details on how to draw these guys in the next two, well-written and easy-to-follow articles: Apollonian Gaskets and Descartes’ Theorem and Apollonian Gaskets and Descartes’ Theorem II.
On Tessellations
Tessellations are like packings … So, stretching the theme a bit, we have this interview with Emily Grosvenor (@emilygrosvenor) about her illustrated children’s book Tessalation! by John Golden (@mathhombre). John also talks about World Tessellation Day which was on June 17th.
The sub trick that kills (On engagement)
Ilona Vashchyshyn (@vaslona) writes in her article on being a substitute teacher
I’ve been substitute teaching for about a month now, which has been a roller-coaster ride (the fun kind). Understandably, most teachers prefer to leave substitutes with a work period. However, I really enjoy engaging with students, especially when math is involved, and so I usually can’t resist showing the students a mathematical “magic” trick that I leave as a challenge for them to figure out during the period. I now have a small collection of tried and true “tricks” that I like to pull out at the beginning of class, but there’s one in particular that kills every. single. time.
In this post, I describe the trick (without revealing the secret) – which can be used as a class starter or warm-up by any teacher, not just a substitute – and discuss why I think students almost always get hooked on trying to figure it out.
Why I Do Math
And finally, Joshua Bowman (@Thalesdisciple) writes this reflective piece on why he does math. He likens it to music and science. He gives an interesting distinction with between mathematics and science: “Math is like science.”
And so concludes this triangular carnival! Next up is Carnival #137 at the AMS Blog on Math Blogs.
Pingback: Meta Blogs on Math Blogs – Study Score Calc
Pingback: Carnival of Mathematics 136 | The Aperiodical
Nice work! Fun collection of mathings.