Did you hear the news? There was an improvement in the “sum-product” problem. Up until a few days ago, I wasn’t even aware that this was a problem of study and research. A few days ago, there was an article on Quanta Magazine explaining both what the sum-product problem is, the current state of research, and the latest “breakthrough”. [As an aside, gosh I wish my PhD got some PR like this!!]
Anyhow, the article is really well-written and fairly accessible to a broad audience.
So what’s a research level problem like this have to do with elementary math education? Well, first let’s quickly go over the problem to keep this article self-contained.
The Sum-Product Problem
- Take a bunch of positive integers of your choosing and however many you want. For example, let’s take [3, 6, 7, 10].
- Make a “sum” grid and a “product” grid like so.
- Count the number of distinct entries in each grid. For the sum grid, there are 9 distinct entries [6, 9, 10, 12, 13, 14, 16, 17, 20] and for the product grid there are 10 distinct entries [9, 18, 21, 30, 36, 42, 49, 60, 70, 100].
Now, the sum-product problem says this: “No matter how many numbers I chose (let’s say I choose \(N\) numbers), the number of distinct entries in the sum grid or the product grid will be close to \(N^{2}\) times some constant.” That is the conjecture! This hasn’t been proved! The latest result put the lower bound at \(N^{\frac{4}{3} + \frac{1}{1055.4}}\). Wikipedia gives a more mathematical statement for anyone curious.
Elementary Math Education?
Ok, now how does this tie in with elementary math education? Am I really proposing that kids work on solving this problem? Clearly not!
However, kids can work on simpler versions of this problem. Mathematicians try their darndest to solve problems in full generality. But sometimes get to a fully general solution we need to explore the “surface area” of the problem. And that means we try out special cases and see what happens.
For elementary students, see if they can find a pattern (ie, a formula) for what happens when they choose
- consecutive numbers (eg, [1,2,3,4] or [1,2,3,4,5] or [6,7,8,9,10,11,12,13])
- consecutive even numbers, consecutive odd numbers
- arithmetic progressions in general
If you’re teaching elementary math, you can immediately see what this does. It does at least this
- exposes students to one aspect of mathematics research — as the teacher / instructor you don’t have to go into great detail, but how exciting is it for students to know that they are legitimately working on a problem that mathematicians are still trying to solve!
- gets in a LOT of number facts practice (addition practice, multiplication practice) without it being a drill for its own sake — that is, they are doing this because they are exploring the structure of such operations (that’s mathematics!!)
- shifts the dialogue about addition and multiplication from the typical tactile and geometric interpretations that are rife in elementary education (not that tactile is bad, but another angle (pun!) is a worthwhile exposure!)
Could it, possibly, start getting students to ask and wonder and explore about the mathematics that they are working on? YES!
Could it bring back some students from their math death? YES!
I know this because I’ve done this many times with young students. The questions they will start asking will be legion. Will it reach every student, every time? No, of course not, but I suspect this is a “high yield” activity.
Finally, if your students aren’t at multiplication just yet, then don’t worry! Just do the exercise with the sum grid!
A few visuals
Here’s what the relationship between the number of consecutive integers and the distinct entries in the sum grid looks like when we start with 1.
And here’s how things look for the product grid for different starting points for consecutive numbers!
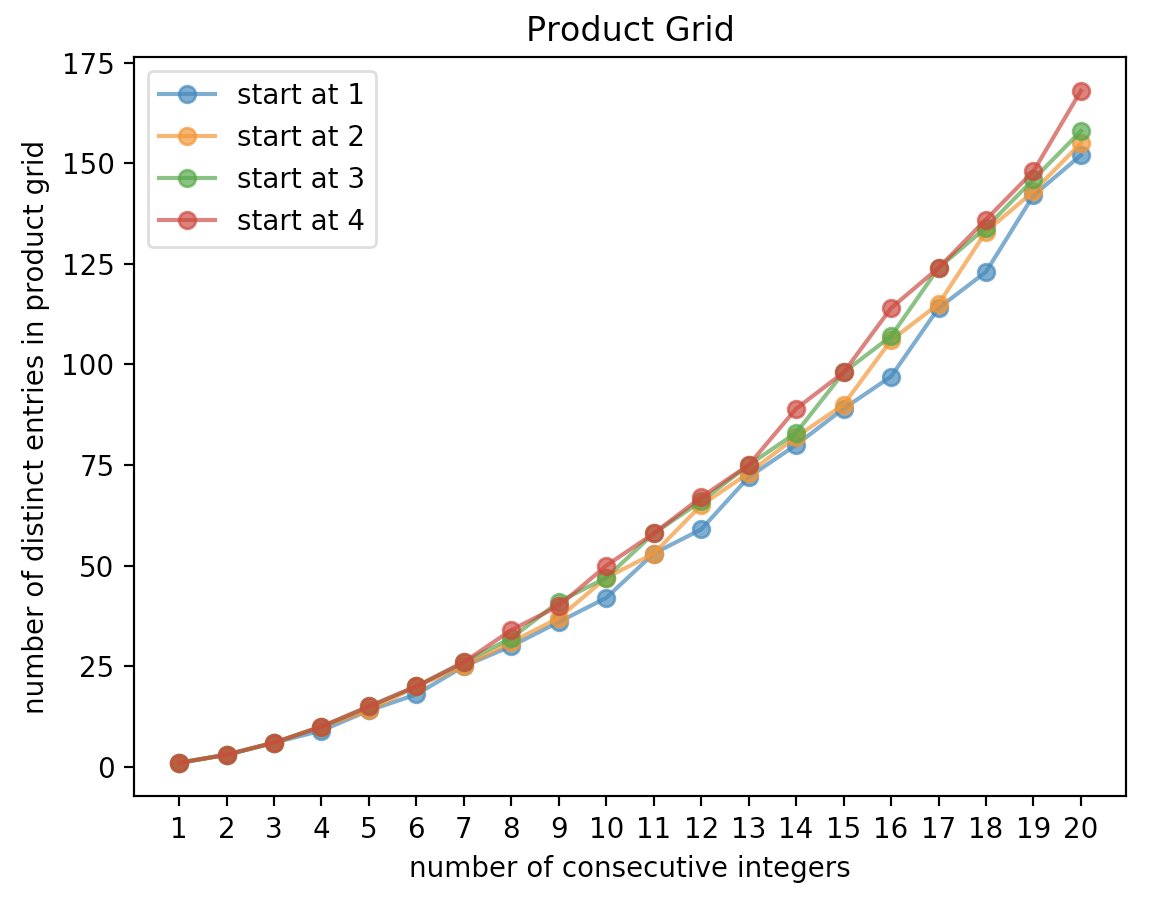


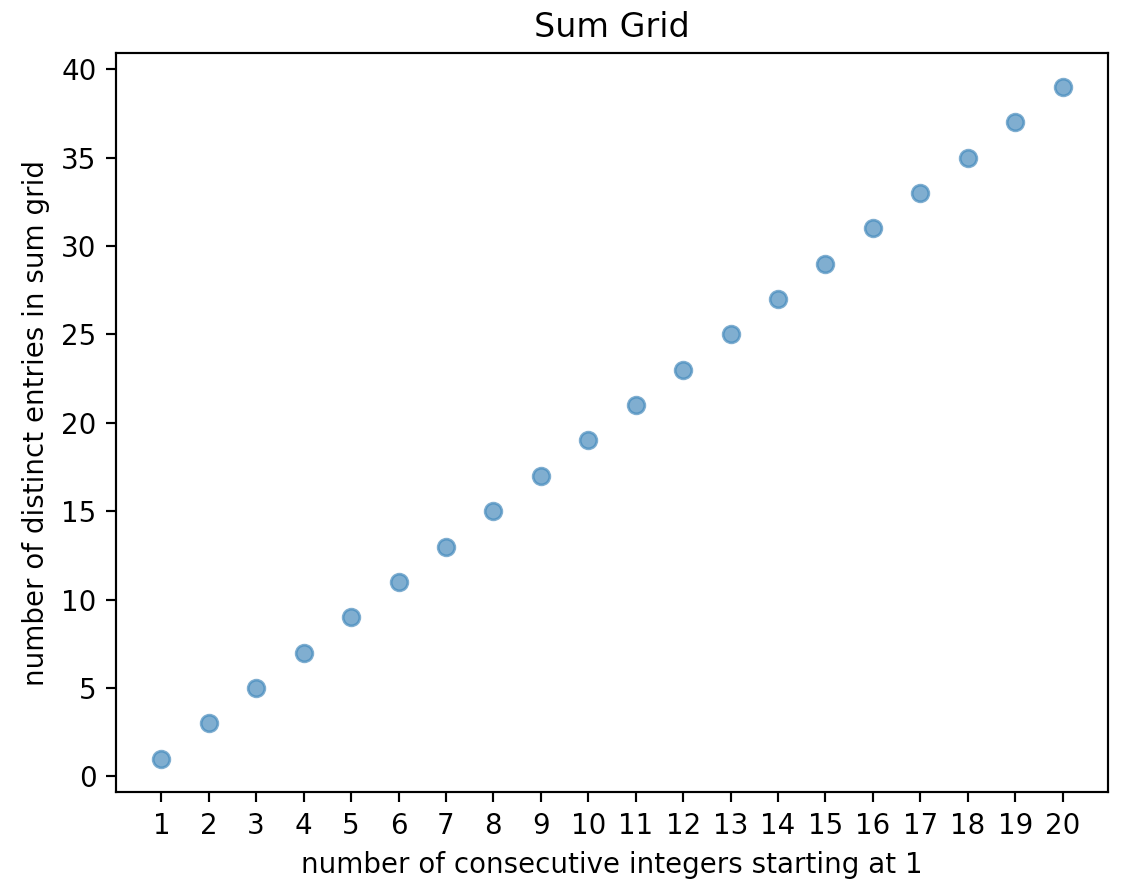
Conjectures are very nice to work on the validity n depth .Euler’s conjecture work by Bose n Shrikhande on BIBD is an example in combinatorics.