What’s fun about numbers? You can do anything you want with them! Add ’em, subtract ’em, stick ’em in a stew. And if you do it well, you’ll get other fun numbers.
Today we’re going to explore probes. These came about from a brilliant typo by @evelynjlamb, in this tweet:
If you don't want to get RTs of primes with a lot of sixes in them for the next few months, you should probably mute me now. I just love the number 6, and so far 6-digit probes starting with 66 have been 🔥
— Evelyn Lamb (@evelynjlamb) November 29, 2019
She meant “primes” as she corrected in a subsequent tweet. But then I decided to get carried away. Why not define a probe?
I mean what is a probe? They’re those things that they launch in Star Trek: Next Generation. Picard is always launching class 1 probes in search of something or to monitor a situation. So here we are. Probes should be numbers that look for other types of numbers.
What types of numbers should we look for? Primes of course!
How should we look for them? And this is where math gets fun.
Here’s how we’ll do it. We’ll pick a natural number \(M\); it will have \(N\) digits in base \(10\) (or if you are a base snob, then pick your damn base) \(d_{1}, d_{2}, \ldots, d_{N}\). For example, if \(M = 2435\), then \(d_{1} = 2, d_{2} = 4, d_{3} = 3, d_{4} = 5\) and \(N = 4\) because there are four digits. Now, we’ll compute this number.
$$2^{4} + 4^{4} + 3^{4} + 5^{4} = 978$$
Now, \(978\) is not a prime number. Therefore, \(2435\) is not a probe.
With that example, we define a probe as a number whose digit-power sum is a prime, where the power is the number of digits. Mathematically,
a positive integer M, with digits, \(d_{1}, d_{2}, \ldots, d_{N}\) is a probe if \(p = \sum_{i=1}^{N}d_{i}^{N}\) is prime.
An example of a probe is \(M = 12\) since \(1^{2} + 2^{2} = 5\), which is a prime.
But what if \(M\) itself is a prime? What then? We’ll call that number a strong probe. And their counterparts are weak probes; that is, \(M\) is a probe, but \(M\) is composite, then \(M\) is a weak probe.
\(2,3,5,7\) are trivially strong probes. \(11\) is our first two-digit strong probe. \(83\) is our last two-digit strong probe as it generates \(73\), which is a prime (verify for yourself!).
In fact, here is the sequence of all strong probes less than \(100\).
\(2,3,5,7,11,23,41,61,83\)
The weak probe sequence begins like this
\(12,14,16,21,25,27,32,38,45,49,52,54,56,58,65,72,78,85,87,94\)
Together, we have the sequence of probes
\(2,3,5,7,11,12,14,16,21,23,25,27,32,38,41,45,49,52,54,56,58,61,65,72,78,83,85,87,94\)
Who probes the probes?
We have a bunch of questions.
Does every prime number have a probe that generates it?
Let’s see, 2 generates 2, 3 generates 3, 5 generates 5, 7 generates 7. But 11? Uh oh. I need to find an \(N\) digit number such that \(d_{1}^N + d_{2}^{N} + \cdots + d_{N}^{N} = 11\). If \(N = 2\) none of the digits can exceed 3 in value and the largest value I can try is 31 (\(3^{2} + 1^{2} = 10\)). I could also try \(23\) or \(32\) but both of these put me over the target of 11. The strong probe condition is even harder because I have to find primes that generate 11. So it doesn’t look like there are 2-digit probes of 11, strong or weak. If \(N = 3\), I can only use the digits \(0,1,2\) and I’m maxed out at \(211\) generating \(2^{3} + 1^{3} + 1^{3} = 10\). Once we get to \(N \geq 4\) we are limited to two digits \(0, 1\). This means that the first probe that generates 11 is \(M = 11,111,111,111\). But this \(M\) is composite (\(513239 \times 21649\)). So it’s not even a strong probe!
We can see by this example, that every prime can be generated by a weak probe and it is trivially simple to find a weak probe for any given target prime.
However, searching for a strong probe that generates 11, in this example, means that we need to search for a prime with exactly eleven 1s and an unknown number of zeros. Which number is that? Your challenge!
Now we turn our attention to strong probes only.
Does every prime number have a strong probe that generates it?
I’m conjecturing this must be true. In the case of generating 11, a strong probe that generates 11 is this 12-digit “binary” prime (apparently primes containing only 0s and 1s they are called Anti-Yarborough): 111,111,111,101. @skrachit finds 101,111,111,111 as the minimal strong probe for 11.
My sense is that just like we can construct a number of only \(N\) ones to generate a probe for prime \(N\), there should always exist an Anti-Yarborough prime with exactly \(N\) ones and an unknown number of zeros that generates a strong probe for prime \(N\).
Since we are searching in the space of integers, we know that there is a minimal strong probe for a target prime \(N\). How we find this minimal strong probe is an interesting problem and I”m sure with a little bit of thought we’ll find some clever ways. As I pointed out for finding a strong probe for 11, we first start with the set of \(K\)-digit numbers and prune this down to a set of viable digits. We saw that if there is a strong probe for 11 in two digits, the largest digit could not exceed 3. For the three-digit case, the largest digit could not exceed 2. And once we reached the four digits or more, we entered into anti-Yarborough territory.
A fun exercise would be to find an algorithm that is not just a brute force, hit-or-miss search when identifying candidate solutions for strong probes.
How many strong probes are there?
“How many” is likely infinite. If every prime number has an anti-Yarborough strong probe, then that strong probe must also have an anti-Yarborough strong probe. Though, I believe that it is an open problem that anti-Yarborough primes are a countably infinite set. But yeah … we need proofs and I’m offering conjectures.
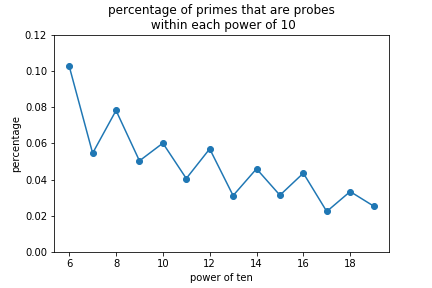
On the other hand … I did a small simulation study for how strong probes are distributed in intervals of \([10^{k}, 10^{k+1})\) and I have this find. I generated random primes in a given power of ten interval and checked if that prime was a strong probe.
So that seems like something to definitely think about as there appears to be a decay and some oscillatory behavior between odd and even powers.
What kind of primes are generated by strong probes?
How convenient that I have a graph for exactly this question.
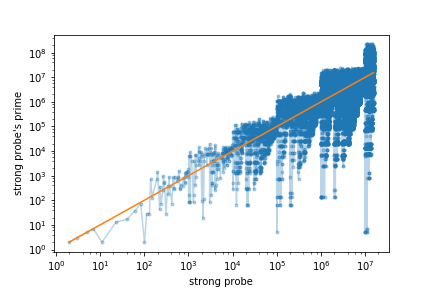
Horizontal axis is the strong probe, vertical axis is the strong probe’s prime. The orange line is the identity \(y = x\)
The primes generated don’t get too out of hand from the strong probe. In fact, if we look at the ratio of the prime generated to the strong probe, we have this [from the first million primes]. So it’ll be a really interesting find if we see a ratio beyond 20.
What are strong probes of order \(K\)?
I don’t know! I didn’t define that for you yet! Let’s consider the prime 11243. It generates 1301, which is prime. Therefore, 11243 is a strong probe. Check. We know this. Now, 1301 generates 83, which is a prime. So 1301 is a strong probe. Oooh. Are you excited? Next, 83 generates 73 which is a prime. So 83 is a strong probe. Finally, 73 generates 58, which is not prime, so 73 is not a probe. And we stop here. What do we have? We have a sequence of strong probes (3 in fact): \(11243 \rightarrow 1301 \rightarrow 83 \rightarrow 73\). Therefore, we call 11243 a strong probe of order 3.
Let’s put down a few theorems without proving them.
Every strong probe is at least of order 1.
If \(M\) is a strong probe of order \(K\), then any permutation of the digits of \(M\) which results in a prime is also a strong probe of order \(K\) (leading zeros are not allowed).
If \(M\) is a strong probe of order \(K\), then any strong probe that generates \(M\) is a strong probe of order \(K+1\).
Some special strong probes
We saw that 2,3,5,7 are strong probes which generate themselves. What shall we call them? How about fixed-point strong probes! I have not been able to find any other fixed-point strong probes. A fixed-point strong probe is redundant. We can simply say fixed-point probe. So either term is ok.
Are there cyclical strong probes?
Or put another way, is it possible to find a strong probe that generates a strong probe that generates a strong probe and so on until one of those strong probes generates a strong probe already found in that sequence? For example, if \(P_{k}\) is a strong probe with index \(k\) [used a few words later], then if \(P_{1}\) generates \(P_{2}\) which generates \(P_{3}\), etc. which generates \(P_{k}\), which then generates \(P_{i}\) for one of the \(i < k\), then we are in a loop. We no longer have a strong probe of order anything. So for this case, we would say that \(P_{1}\) is a cyclical strong probe of order \(k-i-1\) with offset \(i-1\).
While 2 is a fixed-point strong probe, it is also a cyclical strong probe of order 0 with offset 1. \(P_{1} = 2\) which generates \(P_{2} = 2\). Similarly, 11 generates 2 which generates 2, so we have that 11 is a cyclical strong probe of order 0 with offset 1. On the other hand, 101,111,111,111 is a cyclical strong probe of order 0 with offset 2.
Challenge, can you find any cyclical strong probes of order \(K > 0\) with any offset?
I haven’t yet been able to find any.
This my readers is accidental math recreation. I hope you enjoyed this excursion. If you have further explorations of (strong) probes or know some deeper number theory that can answer some of the open questions here, please reach out!

I got behind on my blog reading, so I’m only getting around to this. How delightful to see so much come out of one silly typo!